Performing division is a difficult task as we have seen in case of fixed point arithmetic also. Divider architectures are complex to implement. Floating point division is nothing but a fixed point division with some extra hardwares to take care for the exponents. This extra hardwares make the divider circuit more complex. A floating point division where a number ![]() divides another number
divides another number ![]() can be expressed as
can be expressed as
![]()
Thus it can be said that in a floating point division, mantissas are divided and exponents are subtracted.
The major steps for a floating point division are
- Extract the sign of the result from the two sign bits.
- Find the magnitude of the difference between two exponents (
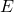 ). Add
). Add 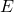 to the bias if
to the bias if 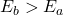 or subtract
or subtract 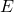 from the bias if
from the bias if 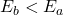 .
. - Divide mantissa of
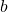 (
( 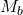 ) by mantissa of
) by mantissa of  (
( 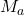 ) considering the hidden bits.
) considering the hidden bits. - If there is a leading zero then normalize the result by shifting it left.
- Due to the normalization, the exponent is to be decremented according to the number of left shifts.
Floating point division can be more clearer with an example. Lets discuss a division operation between two numbers ![]() and
and ![]() . The result of the division operation is
. The result of the division operation is ![]() .
.
Example : Floating Point Division
- Representation: The input operands are represented as
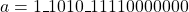 and
and 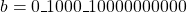
- Sign extraction: As one of the number is negative then sign of the output will be negative. Thus
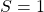 .
. - Exponent subtraction:
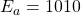 and
and 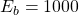 . Thus magnitude of their difference is
. Thus magnitude of their difference is 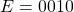 . As
. As 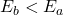 thus the resulted exponent is
thus the resulted exponent is 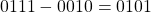 .
. - Mantissa division: Divide the mantissas by any division algorithm used in the fixed point arithmetic. Considering the hidden bits, the division operation is restricted to 12-bits. The result of the division is
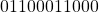 .
. - There is a leading zero in the result thus a left shift can be applied to normalize the result. Thus the new result is
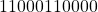 . The final value of the mantissa (
. The final value of the mantissa ( 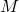 ) is
) is  excluding the hidden bit.
excluding the hidden bit. - The action of normalization step must reflect on exponent correction. The value of the exponent is corrected by a decrement corresponding to a left shift. The new value of the exponent (
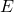 ) is
) is 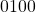 .
. - The final result is
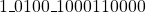 . The decimal value of this is
. The decimal value of this is 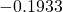 .
.
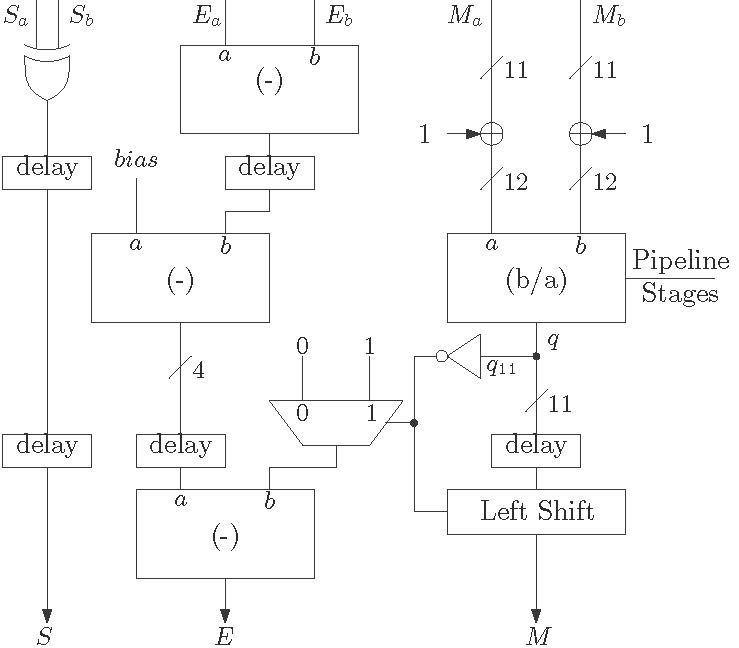
A simple architecture for floating point division is shown below in Figure 1 . There are three 4-bit subtractors used in the divider architecture, two for exponent subtraction and one for correction of exponents. The major hardware block is the divider block. The divider used here is a 12-bit unsigned divider and that can be any divider circuit as discussed in the blog for division. If the result of the divider contains any leading zero then normalizing step is executed. But here in this case, as the hidden bit is also considered thus the result can not go below ![]() . Thus there will be maximum of one leading zero present in the result. This why only the MSB of the result (
. Thus there will be maximum of one leading zero present in the result. This why only the MSB of the result ( ![]() ) is considered and left shift block shifts only by one bit. Pipeline registers are also must be inserted according to the pipe lining stages of the divider.
) is considered and left shift block shifts only by one bit. Pipeline registers are also must be inserted according to the pipe lining stages of the divider.

Can I get the verilog code for this?
Yes you can have….But you have to purchase it.
Hey, willing to pay $ for 32 bit fp divider code. Contact ASAP need it within 2 hours.
We do not provide emergency service here. You have to be happy with whatever we are having here..