Floating Point Multiplication - Digital System Design

Floating point multiplication is comparatively easy than the floating point addition algorithm but off course consumes more hardware than fixed point multiplier circuit. Major hardware block is the multiplier which is same as fixed point multiplier. This multiplier is used to multiply the mantissas of the two numbers. A floating point multiplication between two numbers $a$ and $b$ can be expressed as

${S_b.M_b.2^{E_b}}\times {S_a.M_a.2^{E_a}} = (S_a\oplus S_b).{M_b}\times {M_a}.2^{(E_b + E_a)-bias}$

Thus it can be said that in a floating point multiplication, mantissas are multiplied and exponents are added. The major steps for a floating point division are

Extract the sign of the result from the two sign bits.
Add the two exponents ( 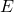$E$ ). Subtract the bias component from the summation.
Multiply mantissa of 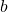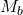$b$ ( $M_b$ ) by mantissa of 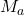$a$ ( $M_a$ ) considering the hidden bits.
If the MSB of the product is 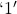$\lq 1\rq \hspace{1pt}$ then shift the result to the right by 1-bit.
Due to this, the exponent is to be incremented according to the one bit right shift.

Floating point multiplication can be more clearer with an example. Lets discuss a multiplication operation between two numbers $b= 6.5$ and $a=3$ . The result of the multiplication operation is $19.5$ .

Example: Floating Point Multiplication

Representation: The input operands are represented as 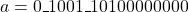$a = 0\_1001\_10100000000$ and $b = 0\_1000\_10000000000$ .
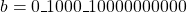Sign extraction: As both the numbers are positive then sign of the output will be positive. Thus $S = 0$ .
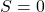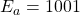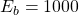Exponent addition: The value of $E_a = 1001$ and $E_b = 1000$ . Thus result of the addition is 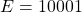$E = 10001$ . The bias is subtracted from this value. Thus new value of 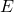$E$ is $1010$ .
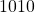Mantissa multiplication: Multiply the mantissas by any multiplicative algorithms used in the fixed point arithmetic. The width of the product is 24-bits but the final output is truncated to 11-bits. The 13-bits of the product starting from the MSB is $1001110000000$ .
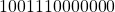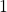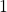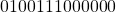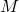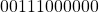Generally the 11-bits from the LSB are the required result but here the MSB is $1$ this indicate that the result is greater than $1$ . Thus this value is shifted right by 1-bit and the new result is $0100111000000$ . The final value of the mantissa ( $M$ ) is $00111000000$ excluding the hidden bit.
This normalization step must reflect on exponent correction. The value of the exponent is corrected by an increment corresponding to a right shift. The new value of the exponent ( 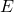$E$ ) is $1011$ .
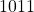The final result is 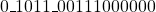$0\_1011\_00111000000$ which is equivalent to 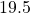$19.5$ in decimal.

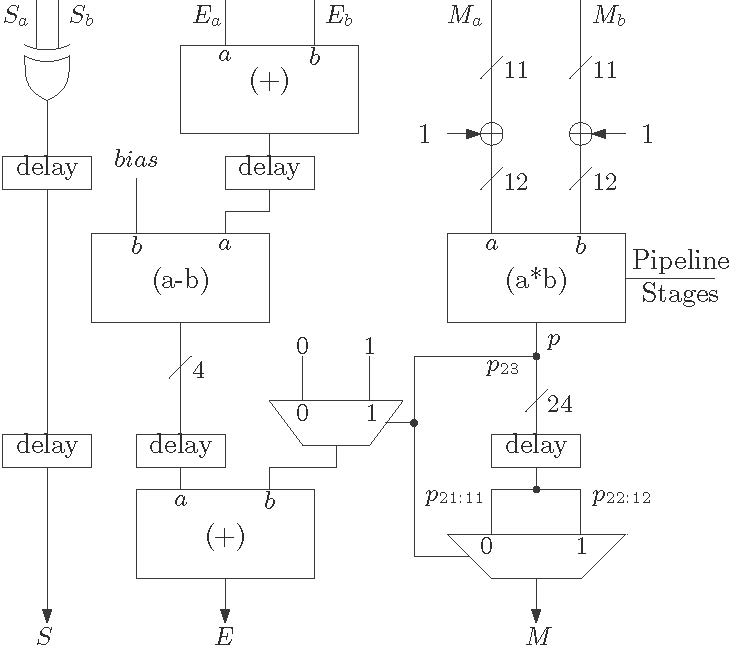
A simple architecture for floating point multiplication is shown below in Figure 1 . The addition of the exponents is done by a 5-bit adder as addition result can be greater than 15. The subtraction of the bias element can be done by another 5-bit adder. There is another 4-bit adder used the design which is actually an incrementer. The major hardware block is the multiplier block. The multiplier used here is a 12-bit unsigned multiplier and that can be any multiplier circuit as discussed in the blog for fast multiplication. If MSB of the product is $1$ then the output is normalized by right shifting. Here this right shift is simply achieved by using MUXes. In this case, as the hidden bit is also considered, the result will be always less than $4$ . Thus only the MSB is checked. Pipeline registers are also must be inserted according to the pipe lining stages of the multiplier.

Figure 1: A Basic Architecture of 16-bit Floating Point Multiplier

-35

Related Posts