Floating Point Square Root - Digital System Design

The architecture for floating point square root computation can also be designed in the same way the other architectures are designed. Various fixed point square root architectures are discussed in the blog for square root computation. There are some modifications needed to convert a fixed point square root architecture to compute square root of floating point numbers. These modifications are mainly related to handling of the exponent field. Square root operation for a floating point number can be expressed as

$\sqrt{0.M_a.2^{E_a}} = 0.\sqrt{M_a}.2^{E_a/2}$

Here the sign field is logic zero which means the square root block always expects positive floating point numbers numbers. The square root operation is carried out only on the mantissa part and this can be achieved by any square root algorithm mentioned in the blog for square root computation . The exponent part is divided by 2 which means right shifting by one bit.

The steps of square root operation for floating point numbers are

Subtract the bias component from the exponent and find the absolute difference.
Right shift the result by one bit then compute the final exponent.
Find the square root of them mantissa with considering the hidden bit.

Example: Square root computation for floating pint numbers.

Square root operation can be more clearer with an example. Lets discuss a square root operation for $a = 8$ .

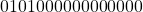The input data $a$ is represented as $0101000000000000$ in 16-bit format.
The absolute difference between the exponent and bias is 3 ( 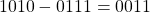$1010 - 0111 = 0011$ ). As $E>bias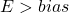$ , the number is greater than 1.
This result is right shifted by 1-bit and this resulted an extra bit ( 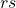$rs$ ) which is 1.
Concatenate the hidden bit with mantissa. Thus the square root block gets 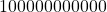$100000000000$ as input.
As the input data is greater than or equal to 1, the input is right shifted by 1 bit so that the fractional square root block can give accurate result.
The output of the square root block is 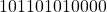$101101010000$ . Thus the value of the mantissa part is $M =01101010000$ .
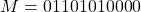The new exponent is $0111 + 0001 = 1000$ .
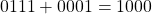Thus the final result is $0100001101010000$ .

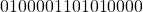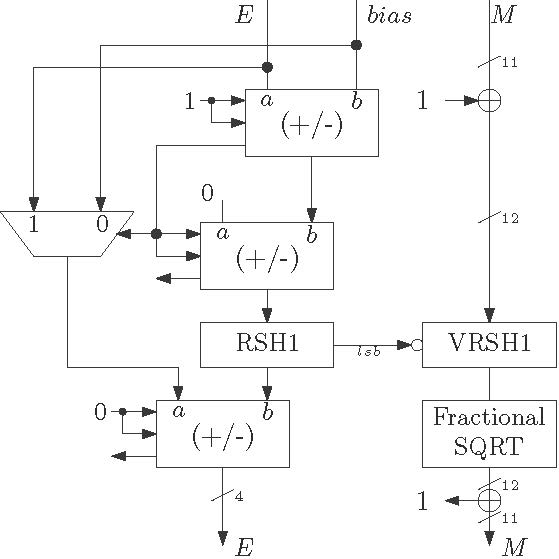
A basic scheme of square root computation for floating pint numbers is shown in Figure 1. Here the architecture is self explanatory. The VRSH1 block is control right shift block. The square root block is capable of computing square root of fractional numbers. In the exponent computation path there is a MUX placed which selects between bias and the exponent of the input number. This is due to the fact that in the square root process exponent of the fractional number should increase with respect to the original exponent.

Figure 1: A basic scheme for square root computation for floating point numbers.

-7

Related Posts