Gaussian Elimination (GE) is one of the most popular methods to solve an linear equation. GE algorithm is the only direct method which is of much interest to the researchers. This method considers that the co-efficient matrix is square. If the matrix ![]() is not square then it can be made square and symmetric as shown for the case of Cholesky decomposition. GE works on the principle of elementary row operation on matrix
is not square then it can be made square and symmetric as shown for the case of Cholesky decomposition. GE works on the principle of elementary row operation on matrix ![]() . Matrix
. Matrix ![]() and
and ![]() are augmented to form matrix
are augmented to form matrix ![]() which is defined as
which is defined as
(1) 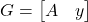
After applying Gaussian Elimination, the matrix ![]() is modified to
is modified to ![]() as
as
(2) 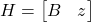
where ![]() is an upper triangular matrix with diagonal elements equal to 1 and column vector
is an upper triangular matrix with diagonal elements equal to 1 and column vector ![]() becomes
becomes ![]() after applying Gaussian Elimination. The estimate
after applying Gaussian Elimination. The estimate ![]() is computed as
is computed as
(3) 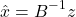
The procedure for making the matrix ![]() into a triangular matrix is important and critical in terms of hardware implementation. The basic equation for elementary row operation is
into a triangular matrix is important and critical in terms of hardware implementation. The basic equation for elementary row operation is
(4) 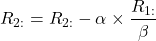
Here, ![]() and
and ![]() denotes first and 2nd row respectively. Here, two new parameters are defined which are
denotes first and 2nd row respectively. Here, two new parameters are defined which are ![]() and
and ![]() . The parameter
. The parameter ![]() indicates the value by which a row is divided and
indicates the value by which a row is divided and ![]() is multiplication factor. Gaussian Elimination technique is illustrated for a
is multiplication factor. Gaussian Elimination technique is illustrated for a ![]() co-efficient matrix. Gaussian Elimination algorithm is accomplished in three steps here. In the first step, row 1 of matrix
co-efficient matrix. Gaussian Elimination algorithm is accomplished in three steps here. In the first step, row 1 of matrix ![]() is divided by
is divided by![]() . The
. The ![]() values for first step are
values for first step are ![]() and
and ![]() . In the second step, row 2 is divided by
. In the second step, row 2 is divided by ![]() . The
. The ![]() value for second step s
value for second step s ![]() . In the last step, row 3 of modified
. In the last step, row 3 of modified ![]() is divided by
is divided by ![]() .
.
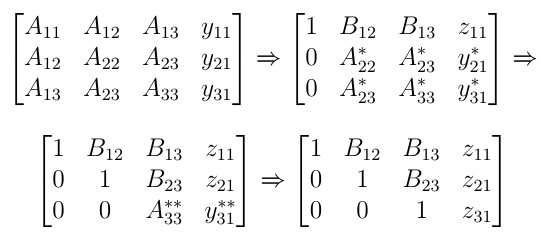
The algorithm for GE is mentioned in Algorithm 1. Input to the algorithm is augmented matrix ![]() .
. ![]() denotes the elements of
denotes the elements of ![]() row of matrix
row of matrix ![]() . GE algorithm is the only direct technique which can be adopted for hardware implementation. Gaussian Elimination has lesser computational complexity than many matrix based factorization techniques. Most hardware expensive operation involved with Gaussian Elimination is division operation. Divider consumes higher logic gates and thus multiple divider can not be used. This is why GE may not be suitable for higher order matrices.
. GE algorithm is the only direct technique which can be adopted for hardware implementation. Gaussian Elimination has lesser computational complexity than many matrix based factorization techniques. Most hardware expensive operation involved with Gaussian Elimination is division operation. Divider consumes higher logic gates and thus multiple divider can not be used. This is why GE may not be suitable for higher order matrices.

