The Non-Restoring (NR) algorithm for square root operation is similar to the NR algorithm for division operation. It is similar to the Restoring algorithm but it has no restoring step. But in implementation of this two algorithms, both are very similar. The NR algorithm for square root operation is shown below in Fig. 1.
In Non-Restoring algorithm for square root, quotient (q) takes value from the digit set {-1,1}. At the output, an on-the-fly conversion is needed to get the actual output. Non-Restoring algorithm is explained with an example in Fig. 2 for the input radicand X = 25/64 (0.011001).
Thus the output is 
. To get the actual output an on-the-fly conversion is needed.
- First mask bits for
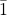. That is Q1 = 0.110. - Then assign Q2 as Q2 = 0.001.
- Subtract Q2 from Q1 to get actual result. That is Q = 0.101 (0.625)
NR algorithm for square root operation with bipolar Q has paved the way for many fast algorithms for square root operation. This may require an on-the-fly conversion but the high speed SRT algorithms are based on this basic NR algorithm. An simpler architecture for NR algorithm for square root is shown below in Fig. 3.
The implementation of NR algorithm is similar to the implementation of Restoring algorithm. Each CAS block is actually a controlled adder/subtractor. Depending upon the status on signal p, CAS block performs addition or subtraction. Same number of CAS blocks are required here as it was in the implementation of Restoring algorithm. This architecture is originally published in [1]. It omits the need of on-the-fly conversion. The authors in [1] also proposed a modular architecture for Non-Restoring algorithm for square root.
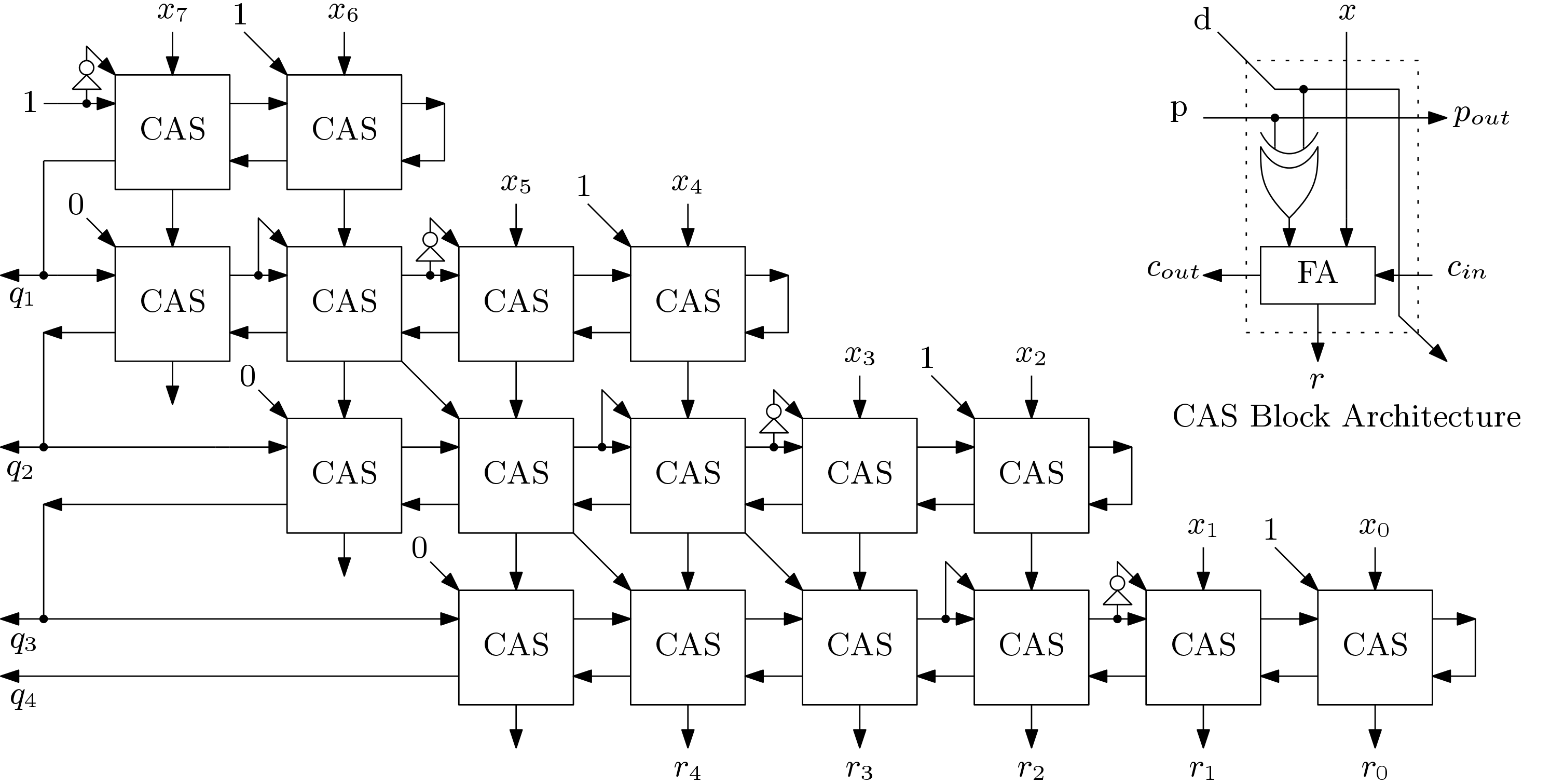
- S. Samavi , A. Sadrabadi, A. Fanian, “Modular array structure for non-restoring square root circuit”, Journal of Systems Architecture, Elsevier, 54 (2008) 957–966
- Click here to download the Verilog code.
