Leading Zero Counter - Digital System Design

In a binary number, leading zeros are the zero digits in the most significant positions of data, up to the position in which the first one is present. For a binary number $x = 0000100011010010$ the leading leading zero count is 4. Leading zero counter is a very important combinational circuit in designing the floating-point architectures to do the normalization operation.

Here an architecture to count maximum 15 leading zeros is presented. A simple modular architecture is presented in [1]. In [1], authors designed higher order leading zero counter using 4-bit leading zero counters. In a binary number ( $x$ ), the leading zero count ( $q$ ) varies from 0 to 3. If all the bits are zero then it generates a signal ( $a$ ) to indicate that the number is zero. The truth table for 4-bit leading zero counter (LZC-4) is shown below in Table 1.

Table 1: Truth Table for 4-bit Leading Zero Counter

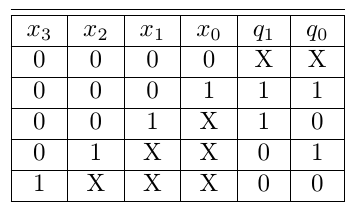
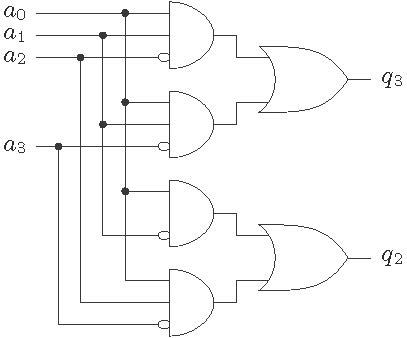
Using the K-map optimization technique the Boolean expression for the outputs of LZC-4 can be obtained and these are

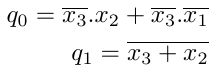
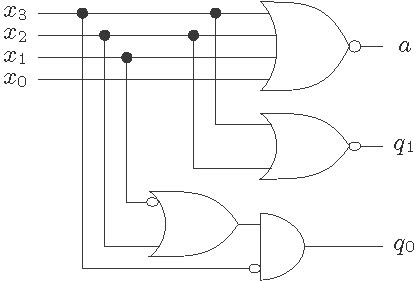
The architecture of the LZC-4 is shown in Figure 1 . It outputs two bits $\{q_1,q_0\}$ and also output an signal $a$ which indicates that all the bits are zero.

Figure 1: A basic architecture for 4-bit Leading Zero Counter

Higher order leading zero counters can be designed using the basic LZC-4 blocks. The four bits are together called as nibble. A 16-bit binary number has four nibbles. The outputs $a_i$ and $z_i$ is generated by the $i^{th}$ nibble from the MSB side. Lets consider to design a LZC-8 block to count 7 leading zeros. In this case, the count will vary from 0 to 7. If $a_0=0$ , the zero count value depends on $z_0$ and if $a_0=1$ then $z_1$ decides the overall count value. The truth table for 16-bit leading zero counter (LZC-16) is shown in Table 2.

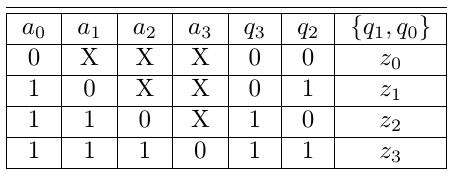
Table 2: Truth Table for 16-bit Leading Zero Counter

The LZC-16 is designed using the basic LZC-4 block. The upper bits of the counter are evaluated by a block which takes the inputs $a_i$ from the LZC-4 blocks. This block is called as leading zero encoder (LZE-4) which is shown in Figure 2. The logical expressions for the outputs of this blocks are decided by the Table 2 . Using K-map the logical expressions are defined as

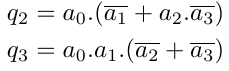
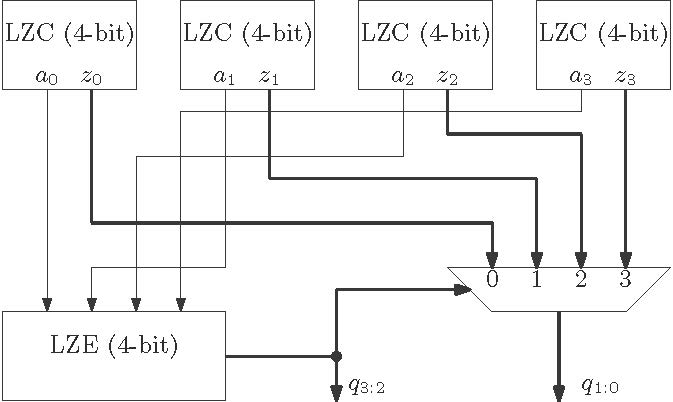
Figure 2: A basic architecture for 4-bit Leading Zero Encoder

Finally the overall architecture of LZC-16 is shown in Figure 3 . There are four LZC-4 blocks used here and one LZE block is used. The output of the LZE-4 block which are the upper bits of the counter selects the lower bits trough a MUX.

Figure 3: A basic architecture for 16-bit Leading Zero Counter

[1]. Nebojša Z. Milenković and Vladimir V. Stanković and Miljana Lj. Milić, “MODULAR DESIGN OF FAST LEADING ZEROS COUNTING CIRCUIT”, Journal of ELECTRICAL ENGINEERING, VOL. 66, NO. 6, 2015, 329–333

Related Posts