Booth’s multiplication algorithm is based on the fact that fewer partial products are needed to be generated for consecutive ones and zeros. For consecutive zeros, a multiplier only needs to shift the accumulated result to the right without generating any partial products. For example, the accumulated result is shifted one bit right for every ‘0’ in the multiplier. This principle can be explained by the help of the following example.
Consider multiplication of two eight bit numbers where A is the multiplicand and the multiplier X takes the value as 00111100. Here X has two repetitive zeros in the left and in the right. The multiplier X has also 4 repetitive ones in the middle. In the general multiplication scheme, a multiplier will need four partial products and each has 8 bits. Total 8 shift operations are required. the repetitive zeros can be dealt with by only shifting the accumulated result. To deal with the repetitive ones, the above multiplication can be written as
![]()
The multiplicand X is written as ![]() . This is the Signed Decimal (SD) representation where
. This is the Signed Decimal (SD) representation where ![]() represents the -1. The partial product -A is added to the accumulated result due to the presence of
represents the -1. The partial product -A is added to the accumulated result due to the presence of ![]() in the newly modified X. Thus in this case, instead of four partial products only two partial products are needed. The number of shifting operations remains same.
in the newly modified X. Thus in this case, instead of four partial products only two partial products are needed. The number of shifting operations remains same.
The above mentioned technique is called Booth’s recoding the multiplier in SD form. In this technique, current bit ![]() and the previous bit
and the previous bit ![]() of the multiplier
of the multiplier ![]() ..
..![]() is checked to generate the current bit
is checked to generate the current bit ![]() of the recoded multiplier
of the recoded multiplier ![]() ..
.. ![]() . A simple way of recoding is by the equation
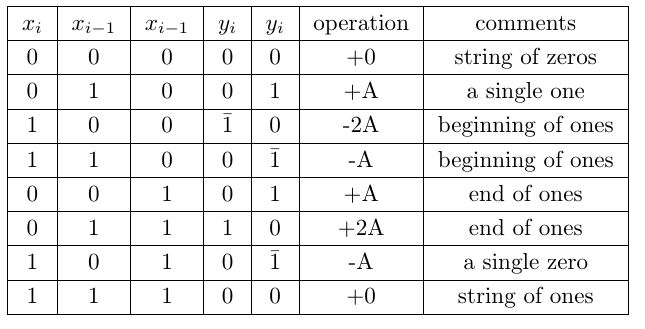
. A simple way of recoding is by the equation ![]() . This technique of recoding is also called as Booth’s Radix-2 recoding method. Recoding need not to be done any predefined manner and can be done in parallel from any bit positions. The simplest recoding scheme is shown in Table 1.
. This technique of recoding is also called as Booth’s Radix-2 recoding method. Recoding need not to be done any predefined manner and can be done in parallel from any bit positions. The simplest recoding scheme is shown in Table 1.

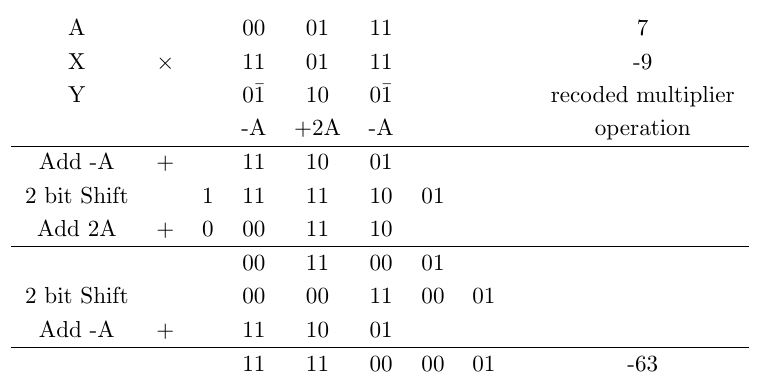
An example of multiplication using Booth’s radix-2 algorithm is shown below in Table 2 for two 4-bit signed operands. Here recoding is started from the LSB. The computation of Y is not necessary as it involves extra hardware. Instead the adder and subtractor blocks are controlled accordingly.

There are two drawbacks of this Booth’s algorithm which are
- The number add/sub operation is not fixed and also the number of shift operations between two add/sub operations is not fixed.
- The algorithm is not efficient when there is isolated ones. For example
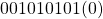 is recoded as
is recoded as 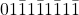 which increases the add/sub operations instead of reducing it.
which increases the add/sub operations instead of reducing it.
Radix-4 Booth’s Algorithm:- The disadvantages of the Radix-2 algorithm is improved by the Radix-4 Booth’s algorithm. Here three bits are examined instead of two bits. The bits ![]() and
and ![]() are recoded into
are recoded into ![]() and
and ![]() while
while ![]() act as reference bit. The variable i takes the value from the set {1,3,5….} . The recoding of the multiplier can be done easily by the following equation
act as reference bit. The variable i takes the value from the set {1,3,5….} . The recoding of the multiplier can be done easily by the following equation
![]()
The scheme of recoding of the multiplier in the Booth’s Radix-4 algorithm is shown in Table 3. The Radix-4 algorithm efficiently overcomes all the limitations of the Radix-2 recoding algorithm. In this multiplication process, total three add/sub operations is performed. Hence the Radix-4 algorithm takes total n/2 add/sub operations. In each operation, two bits are dealt with and shifting operation is of two bits.
Canonical Recoding :- The number of add/sub operations in a multiplier depends on the optimum SD representation of the multiplier (X). In other way, the number of non zero elements in Y decides the number of add/sub operations. The SD representation of the multiplier in Booth’s Radix-2 and Radix-4 algorithm is not optimum. Canonical recoding algorithm is a technique which obtains an optimum representation of a multiplier. Canonical recoding algorithm operates on a multiplier from right to left on one bit a time. Here ![]() serves as a reference bit. A multiplier (X) represented in two’s compliment form is treated as
serves as a reference bit. A multiplier (X) represented in two’s compliment form is treated as ![]() ….
…. ![]() to obtain optimum SD representation.
to obtain optimum SD representation.
Unlike the Radix-2 and Radix-4 algorithm, Canonical recoding algorithm includes carry input to obtain SD representation. Here ![]() is the carry input and
is the carry input and ![]() is the carry output. The different rules of obtaining optimum representation is shown below in the Table 5. The SD representation of the multiplier X = 01101110 in Radix 2 algorithm is
is the carry output. The different rules of obtaining optimum representation is shown below in the Table 5. The SD representation of the multiplier X = 01101110 in Radix 2 algorithm is ![]() . The optimum SD representation of this multiplier in Canonical recoding algorithm is
. The optimum SD representation of this multiplier in Canonical recoding algorithm is ![]() .
.
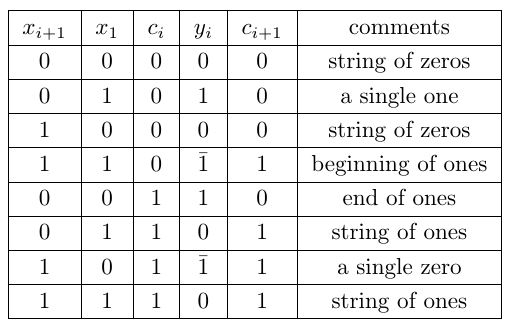
There are mainly two disadvantages of Canonical recoding algorithm.
- The bits of the recoded multiplier is obtained sequentially as it involves carry generation and propagation.
- The second disadvantage is same as it is for Radix-2 algorithm that is optimum SD representation corresponds to variation in number of add/sub operations.
An Alternative 2-bit at a Time Multiplication Algorithm :- An alternative algorithm exists to reduce the partial products by involving fixed number of add/sub operations. This algorithm is similar to the Radix-4 algorithm and operates on two bits at a time. In this algorithm, the ![]() is considered as reference bit and the recoded multiplier Y can be computed in parallel. Total number of add/sub operations is always n/2. The rules for this algorithm is shown Table 6. Here the multiple of A can be obtained easily by wired shifting.
is considered as reference bit and the recoded multiplier Y can be computed in parallel. Total number of add/sub operations is always n/2. The rules for this algorithm is shown Table 6. Here the multiple of A can be obtained easily by wired shifting.
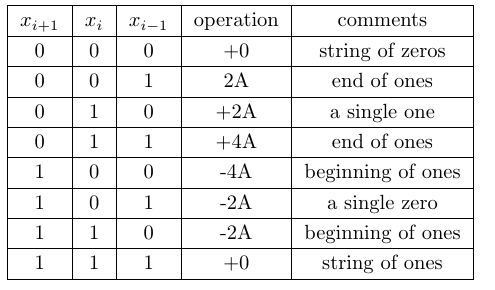
In this algorithm as the reference bit is ![]() , it ignores if there is a start of string of ones in the right most pair
, it ignores if there is a start of string of ones in the right most pair ![]() . A correction step is needed in this algorithm. This is described in Table 7.
. A correction step is needed in this algorithm. This is described in Table 7.
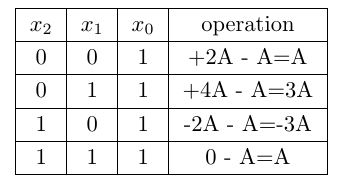
This alternative algorithm provides easy recoding rules compared to the original Radix-4 algorithm but it has a correction step. Initially there is decision to make to select between A or 3A. The computation of 3A involves an extra add/sub operation.

Thanks ᴠery interesting blog!