Signal processing algorithms sometimes involve computation of exponential as well as logarithm. Thus it is important to implement both the functions on digital hardware. In our previous tutorials, we have discussed implementation of exponential function. In this work, design of digital hardware to find logarithm of a number is discussed. The logarithm function is computed by multiplicative iterative formulas.
The computation of logarithm of a number is governed by the following equations
(1) 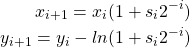
where ![]() varies from 0 to
varies from 0 to ![]() . A new parameter
. A new parameter ![]() is defined which is evaluated as
is defined which is evaluated as
(2) 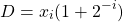
The control parameter ![]() is evaluated as
is evaluated as
(3) 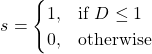
When ![]() the equations (1-2) is modified a
the equations (1-2) is modified a
(4) 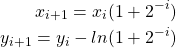
and when ![]() the equation (1-2) becomes
the equation (1-2) becomes
(5) 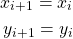
After ![]() iterations the final values of
iterations the final values of ![]() and
and ![]() are
are
(6) 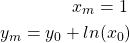
In other way, the following equation is also true
(7) 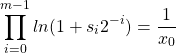
The range of within which the logarithm is computed is ![]() .
.
This range is small but logarithm of any number can be found if it is normalized to this range. Let’s discuss computation of two such numbers which are out of the range.
Example 1: Consider binary value of input data is ![]() .
.
- Step 1: Normalize the data.
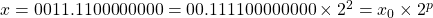 .
.
- Step 2: Find logarithm of fractional data.
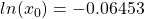 .
.
- Step 3: The logarithm of
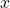 can be expressed as
can be expressed as 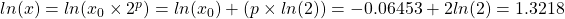
Example 2: Consider binary value of input data is ![]() .
.
- Step 1: Normalize the data.
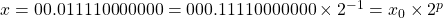 .
.
- Step 2: Find logarithm of fractional data.
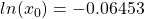 .
.
- Step 3: The logarithm of
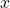 can be expressed as
can be expressed as 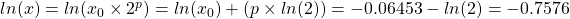 .
.
The above discussion was to find the logarithm of number with base ![]() . But logarithm of a number with any base can be found easily by storing the data in ROM with respect to that base.
. But logarithm of a number with any base can be found easily by storing the data in ROM with respect to that base.
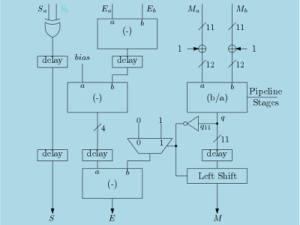
Hardware Implementation of Logarithm Function
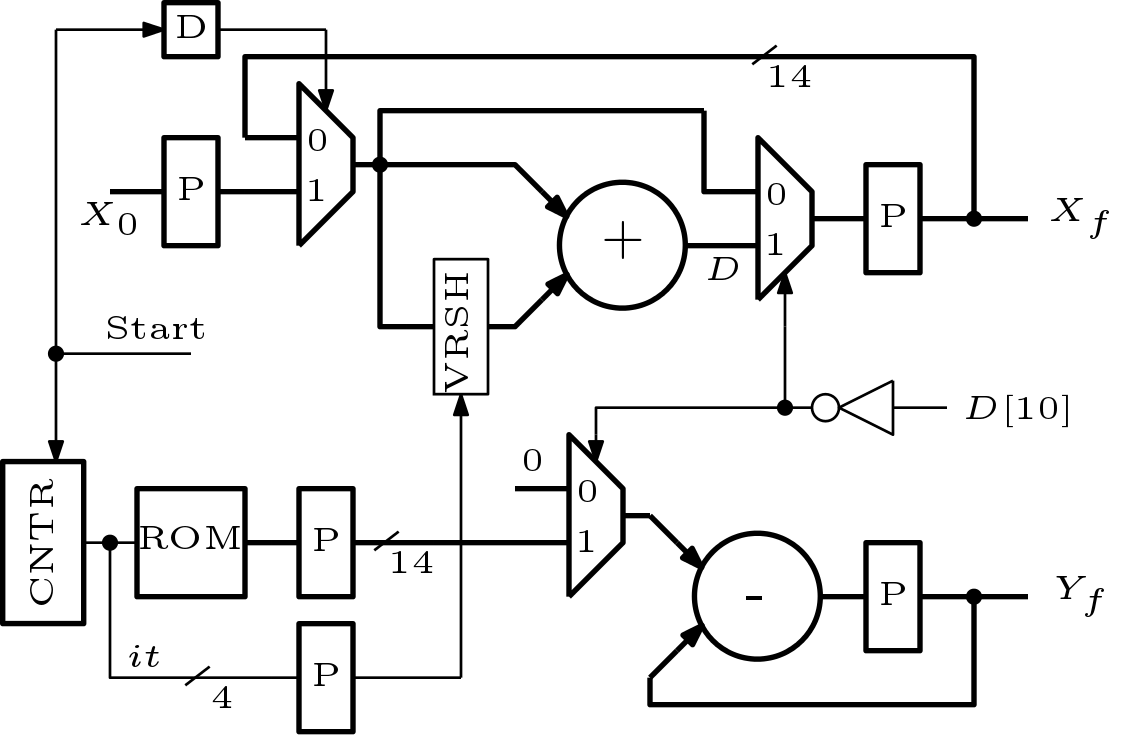
The hardware implementation of logarithm is very similar to the architecture of efficient exponential architecture which described in our previous post. The architecture is shown in Figure 1. Here, ROM stores the values of ![]() . The VRSH block is responsible for variable shift by any number from 0 to 15. The signal
. The VRSH block is responsible for variable shift by any number from 0 to 15. The signal ![]() indicates that the value of
indicates that the value of ![]() is not greater than 1. Initially,
is not greater than 1. Initially, ![]() should be loaded to a register and the values of
should be loaded to a register and the values of ![]() and
and ![]() should be cleared. The architecture shown here uses 14-bits but 12 bits are enough if 10-bit precision is required. The
should be cleared. The architecture shown here uses 14-bits but 12 bits are enough if 10-bit precision is required. The ![]() block provides address to the ROM block as well as provides shifting count to the VRSH block.
block provides address to the ROM block as well as provides shifting count to the VRSH block.