In the previous post, we have discussed the theory for computation of exponential and discussed about its hardware architecture. In this post, we will discuss an alternative architecture to compute the exponential. If we examine the equations which evaluate the exponential function, then we can see that ![]() is multiplied by
is multiplied by ![]() or
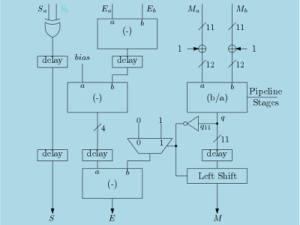
or ![]() . In the previous architectures, we have used a multiplier to do this multiplication. But do we need a dedicated multiplier here? the answer is no. As the multiplication here is done by only power of 2 and multiplication by power of 2 can be done by wired shifting. Thus in this post we have shown here an efficient architecture which omits the need of a multiplier. The architecture for exponential function is shown in Figure 1.
. In the previous architectures, we have used a multiplier to do this multiplication. But do we need a dedicated multiplier here? the answer is no. As the multiplication here is done by only power of 2 and multiplication by power of 2 can be done by wired shifting. Thus in this post we have shown here an efficient architecture which omits the need of a multiplier. The architecture for exponential function is shown in Figure 1.
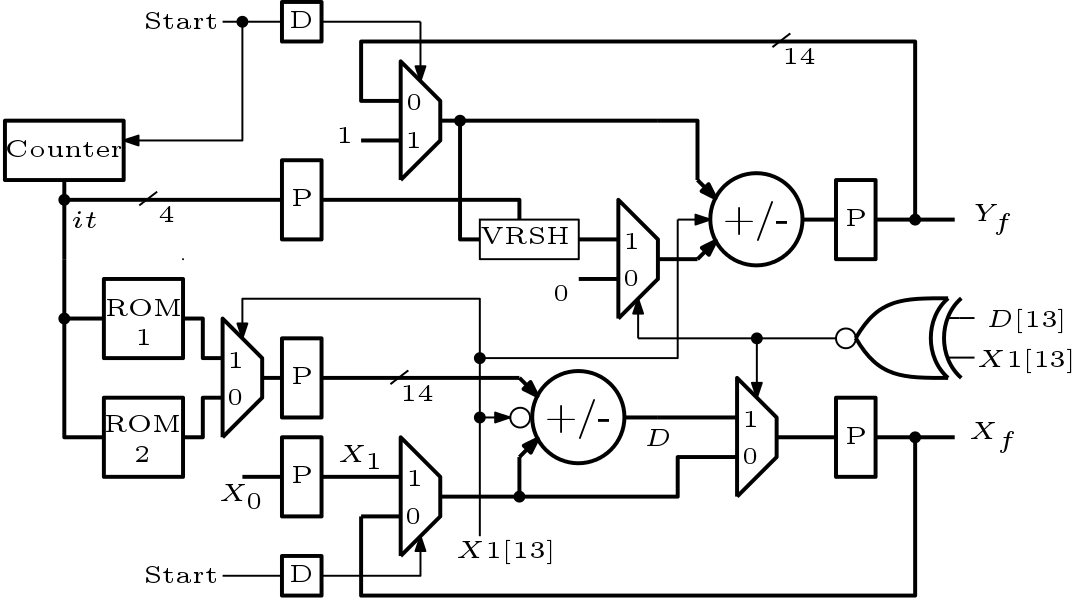
Here a new block is introduced which is called VRSH. It is a variable right shift block. More about this type of blocks is discussed in our previous post for combinational circuits. This block can shift the input data by any number from 0 to 15. The output of the counter is delayed and it is given as input to the VRSH block. This input decides how much shift will take place. The multiplexer next to the VRSH block can be replaced by a tristate buffer also. In place of a multiplier, another add/sub block is used here. Thus this architecture is hardware efficient compared to the architectures discussed previously. This architecture now becomes similar to the architecture of serial CORDIC. The parallel and pipeline architecture of this scheme can be easily adopted.
But this circuit has its own problems too. Just like the serial CORDIC architecture, this architecture also has a high critical path and this path is MUX-VRSH-MUX-ADD/SUB. This path limits the speed of operation.
Verilog Code for Efficient Architecture of Exponential (4039 downloads )