Signal processing algorithms sometimes involve computation of exponential. Thus it is important to implement the exponential function. In this work, design of digital hardware for exponential function is discussed. Like other elementary functions, exponential function is also computed using the iterative formulas. In this work, computation of the exponential function ![]() is shown for three cases.
is shown for three cases.
- When
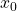 is positive.
is positive. - When
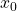 is negative.
is negative. - When
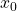 is positive or negative.
is positive or negative.
1. Computation of 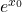 when
when 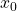 is Positive
is Positive
The computation of ![]() is governed by the following two equations.
is governed by the following two equations.
(1) 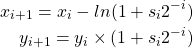
where ![]() varies from
varies from ![]() to
to ![]() which is the total number of iterations. Initially,
which is the total number of iterations. Initially, ![]() and
and ![]() . A new parameter
. A new parameter ![]() is defined to find the values of
is defined to find the values of ![]() . It is computed as
. It is computed as ![]() .
.
(2) 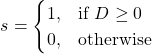
When ![]() the equations (1) is modified as
the equations (1) is modified as
(3) 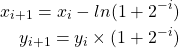
and when ![]() the equation (1) becomes
the equation (1) becomes
(4) 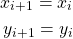
After ![]() iterations the final values of
iterations the final values of ![]() and
and ![]() are
are
(5) 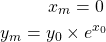
In other way, the following equation is also true
(6) 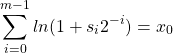
Implementation of Exponential Function for Positive Values
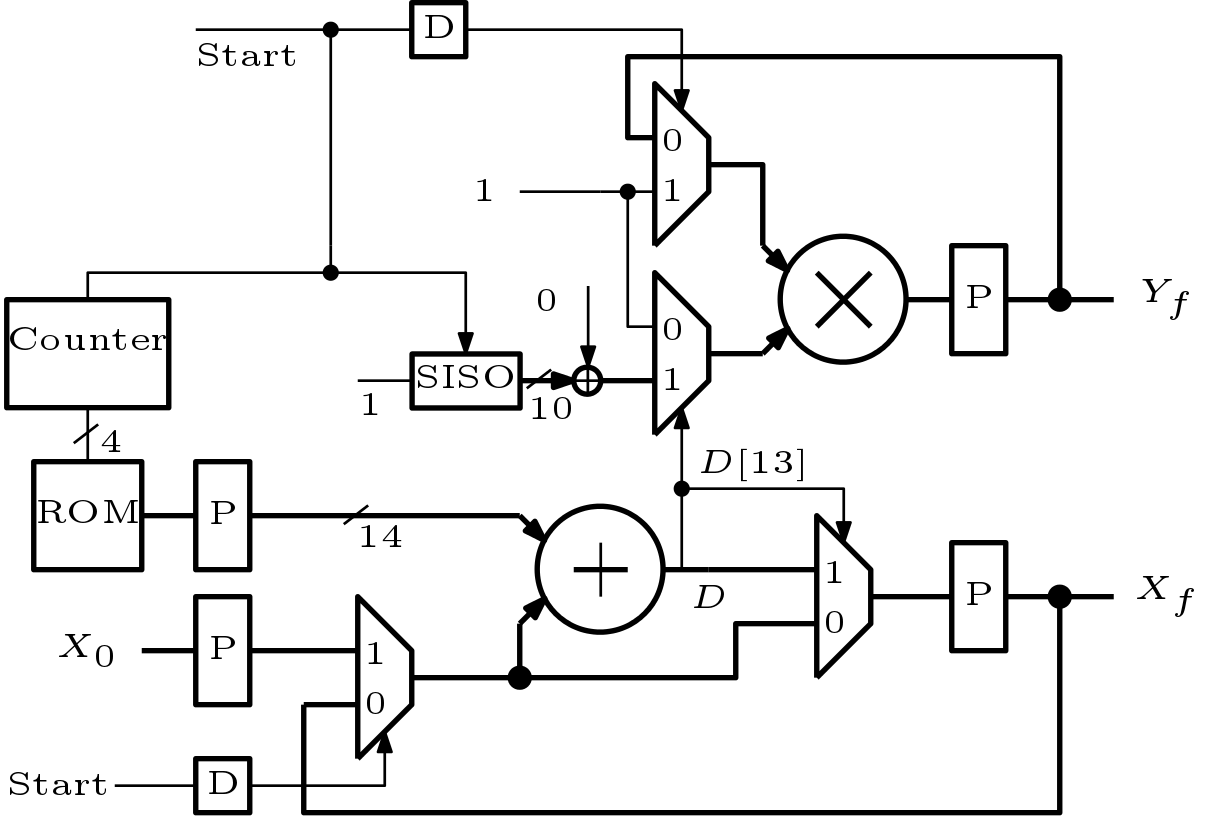
Based on the above equations, a serial architecture is developed in this work to compute ![]() when
when ![]() is positive. The architecture is shown in Figure 1. The minimum data-width which is required in this architecture is 14 to support all the results. Out of 14-bits, 10-bits are used for fractional part. Total 11 iterations are required. The values of
is positive. The architecture is shown in Figure 1. The minimum data-width which is required in this architecture is 14 to support all the results. Out of 14-bits, 10-bits are used for fractional part. Total 11 iterations are required. The values of ![]() for 10-bit precision is shown in Table 1. These values are stored in ROM and size of it is
for 10-bit precision is shown in Table 1. These values are stored in ROM and size of it is ![]() . Initially a
. Initially a ![]() signal loads
signal loads ![]() in a register and starts the counter. The delayed version of
in a register and starts the counter. The delayed version of ![]() signal chooses initial value ‘1’ for the multiplier and also chooses
signal chooses initial value ‘1’ for the multiplier and also chooses ![]() as initial value to the subtracter. A Serial Input Serial Output (SISO) is used to generate the values of
as initial value to the subtracter. A Serial Input Serial Output (SISO) is used to generate the values of ![]() . The symbol
. The symbol ![]() in Figure 1 indicates concatenation operation. This operation take place like the following way
in Figure 1 indicates concatenation operation. This operation take place like the following way
![]()
Where ![]() signal indicates iteration zero or first iteration. Computation of next data is started by clearing the final values of
signal indicates iteration zero or first iteration. Computation of next data is started by clearing the final values of ![]() and
and ![]() . The new value of
. The new value of ![]() is again stored in the register. At least 12 clock cycles are required in computation of one exponential function.
is again stored in the register. At least 12 clock cycles are required in computation of one exponential function.
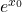 when
when 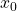 is positive.
is positive.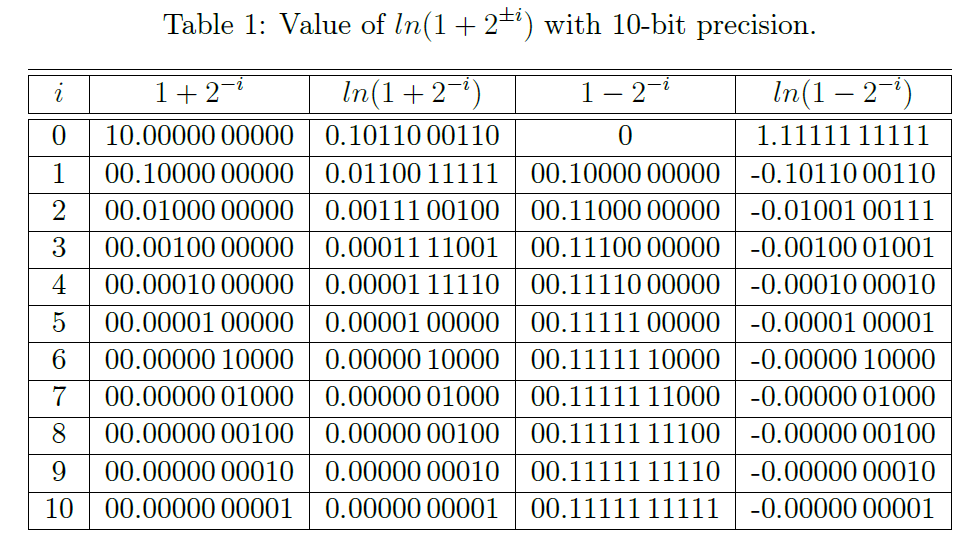
2. Computation of 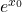 when
when 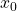 is Negative
is Negative
The computation of ![]() when
when ![]() is negative is done in the same way as it was computed in the previous section. The parameter
is negative is done in the same way as it was computed in the previous section. The parameter ![]() is computed as
is computed as ![]() .
.
(7) 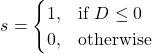
When ![]() the equations (1) is modified as
the equations (1) is modified as
(8) 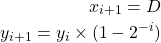
The equation (1) when ![]() is same for both the cases. The final equations are also same.
is same for both the cases. The final equations are also same.
The range of ![]() is is controlled by the following equation
is is controlled by the following equation
(9) 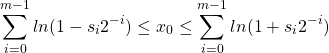
thus the range of ![]() is
is ![]() .
.
Implementation of Exponential Function for Negative Values
Architecture to compute ![]() when
when ![]() is negative is very similar to the architecture discussed previously. The architecture is shown in Figure 2. Here ROM stores the values of
is negative is very similar to the architecture discussed previously. The architecture is shown in Figure 2. Here ROM stores the values of ![]() as shown in Table 1. The size of the ROM is 1-bit higher than the ROM which was previously used to store
as shown in Table 1. The size of the ROM is 1-bit higher than the ROM which was previously used to store ![]() . In place of subtracter, an adder is used here. The concatenation operation take place like the following way
. In place of subtracter, an adder is used here. The concatenation operation take place like the following way
![]()
In order to compute the exponential of next value of ![]() , the values of
, the values of ![]() and
and ![]() must be cleared. The SISO is also needed to cleared.
must be cleared. The SISO is also needed to cleared.
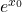 when
when 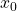 is negative.
is negative. 3. Computation of 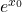 when
when 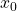 can be +ve or -ve
can be +ve or -ve
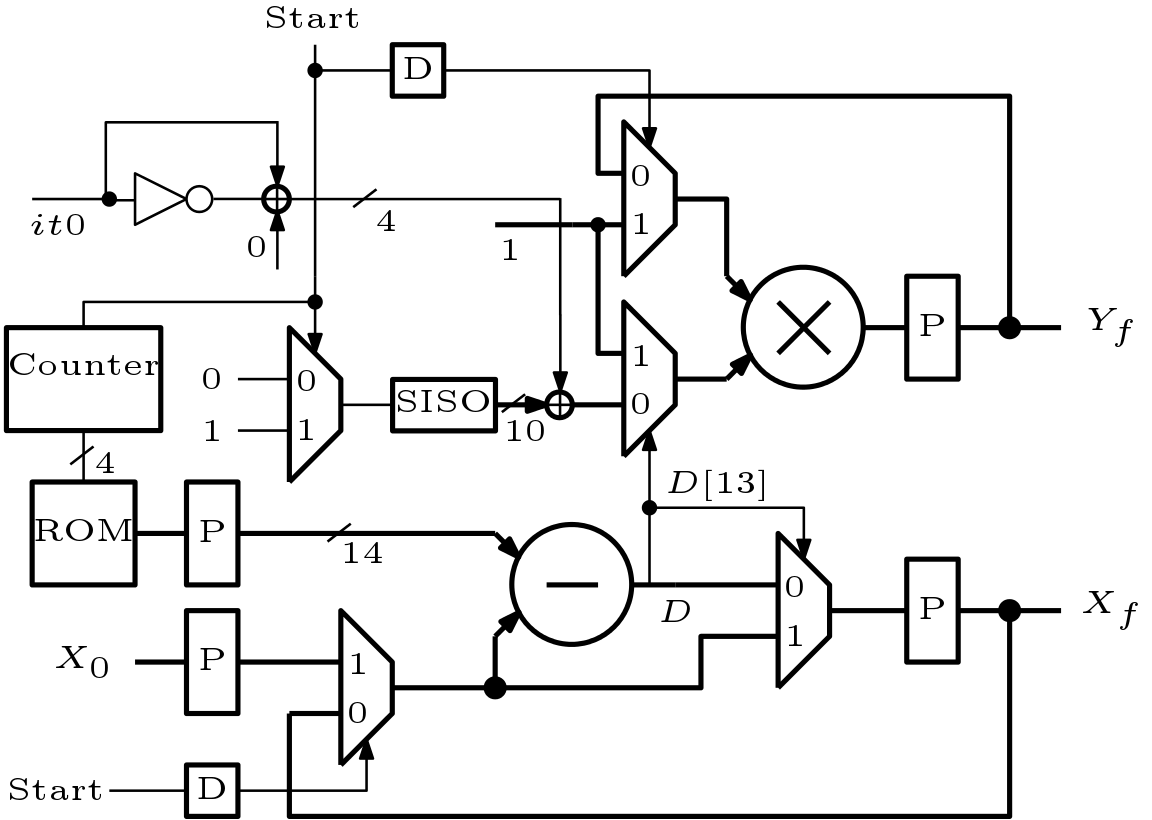
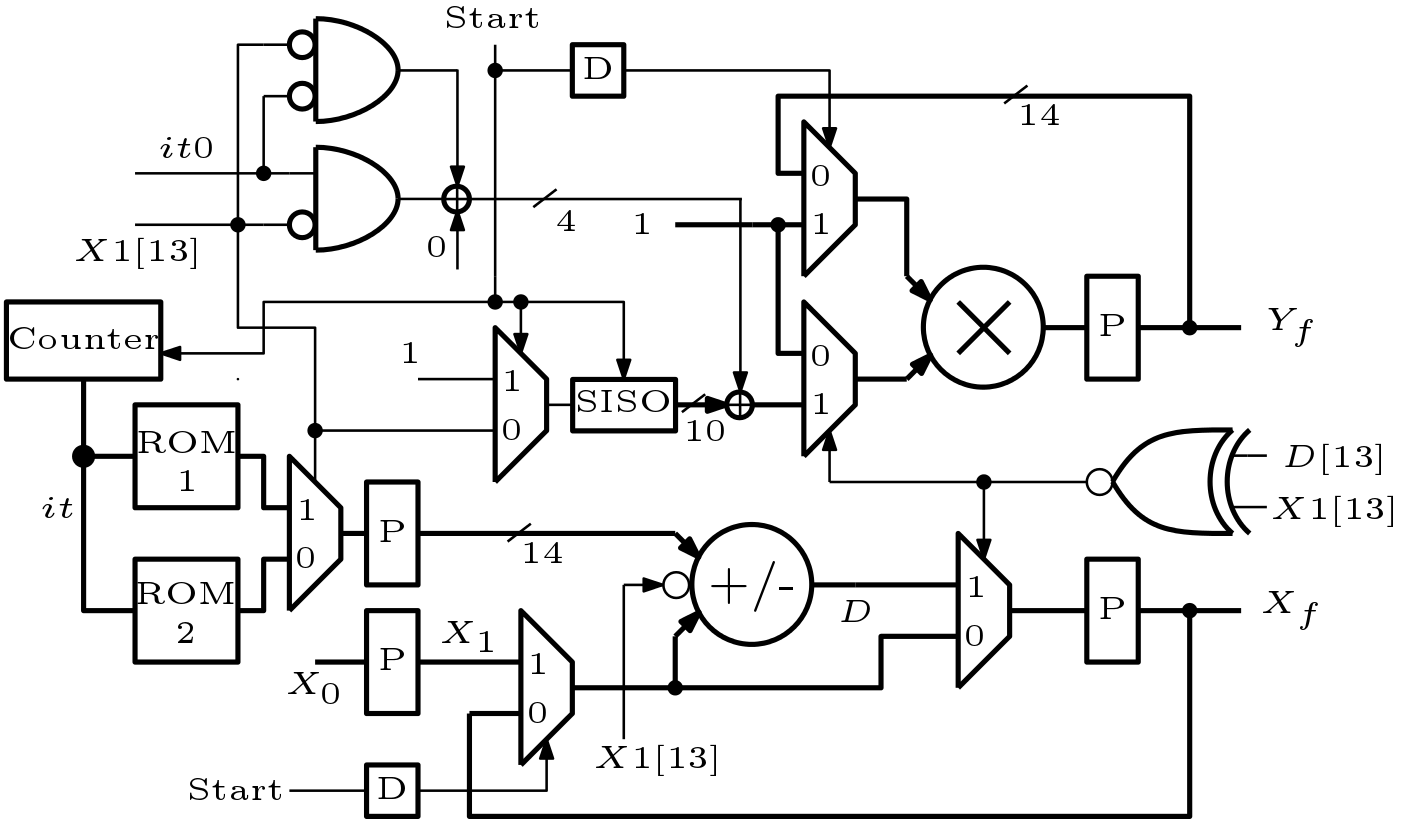
It is important to compute ![]() by a same hardware when
by a same hardware when ![]() can be both positive or negative. Thus Figure 1 and Figure 2 is combined and a new architecture is developed which is shown in Figure 3. Two ROMs are used here. ROM 1 stores values of
can be both positive or negative. Thus Figure 1 and Figure 2 is combined and a new architecture is developed which is shown in Figure 3. Two ROMs are used here. ROM 1 stores values of ![]() and ROM 2 stores values of
and ROM 2 stores values of ![]() . If
. If ![]() is negative then data is read from ROM 1. An adder/subtracter is used here which is controlled by invert of the MSB of
is negative then data is read from ROM 1. An adder/subtracter is used here which is controlled by invert of the MSB of ![]() .
.
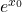 when
when 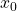 can be both positive or negative.
can be both positive or negative.Conclusion
Computation of exponential function can be done by other methods also like CORDIC but this method is more accurate than the CORDIC based method. The range of exponential function can be increased by scaling of input data and by including a post scalar block.
