Signed Array Multiplier

In the previous tutorials, a scheme of Unsigned Array Multiplier is discussed. Unsigned Array Multiplier may be useful when we are concerned only about unsigned numbers. But in majority of digital systems, operands can be signed or unsigned and thus a dedicated signed array multiplier is needed. This signed array multiplier can perform multiplication for both signed and unsigned numbers.

Array multiplier resembles the pen and paper method of multiplication process which is shown in previous tutorials. An array of full adders are used for the unsigned multiplication process. For -bit data width, total full adders are used in this multiplier. Carry outputs of a stage is added in the next stage to form a systolic architecture. But in the last stage carry is used in the same stage to reduce hardware. At the first stage, the FAs can be replaced with HAs but here FA blocks are retained.

The signed multiplication is little bit complicated than the unsigned array multiplication. In case of 4-bit signed multiplication where the operands are represented in Two’s complement representation, instead of adding the product bits or should be subtracted. This is because the MSB bit in 4-bit operand is signed bit. Array multipliers are designed to handle such bits and a Sub block (SB) is designed. The basic operation of this block is

The boolean expressions become upon simplifying using K-map as

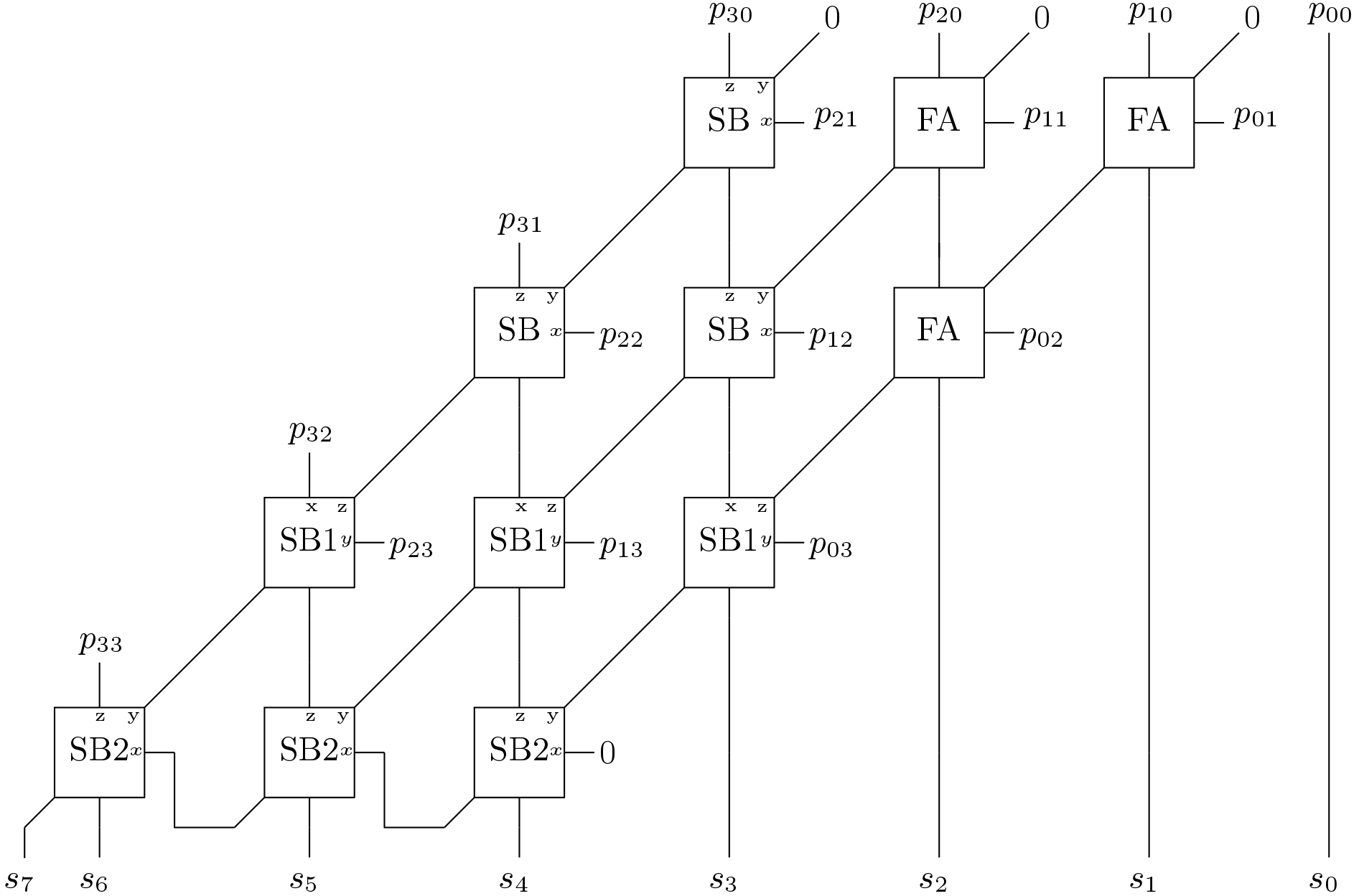
The expressions are similar to that of the FA but negative bit is inverted in the computation of carry. The signed array structure is shown in Figure 1. Here, three type of SB blocks are shown but their logic expressions are same. In case of SB, is the negative bit. But in case of SB1 and SB2, and are the negative bits.

+3

0