Newton-Raphson’s iterative algorithm is a very popular method to approximate a given function. It can be used to compute reciprocal of a given number. The Newton-Raphson’s iterative equation is
![]()
where ![]() is the first derivative of
is the first derivative of ![]() . The function which is used to compute the reciprocal of a number is
. The function which is used to compute the reciprocal of a number is ![]() , where D is the input operand. The Newton-Raphson iteration gives
, where D is the input operand. The Newton-Raphson iteration gives
![]()
After some finite iterations the above equation converges to the reciprocal of D. It is very obvious that initial value of X ( ![]() ) must be chosen care fully to converge. The value of D is scaled to be in the range
) must be chosen care fully to converge. The value of D is scaled to be in the range ![]() to chose the initial guess
to chose the initial guess ![]() such that few number of iterations required for computation. In this case, D is shifted right or left to be in that range. In that interval of D, one must chose initial value
such that few number of iterations required for computation. In this case, D is shifted right or left to be in that range. In that interval of D, one must chose initial value ![]() as
as
![]()
The architecture for Newton-Raphson based reciprocal computation is shown below. A serial architecture is given here as parallel architecture is costly and most system architectures uses serial architecture. The pulsed control signal start starts the iteration and ![]() is the final result. If D is not in the range, pre-processing is required and at the output a post-processing step is also required.
is the final result. If D is not in the range, pre-processing is required and at the output a post-processing step is also required.
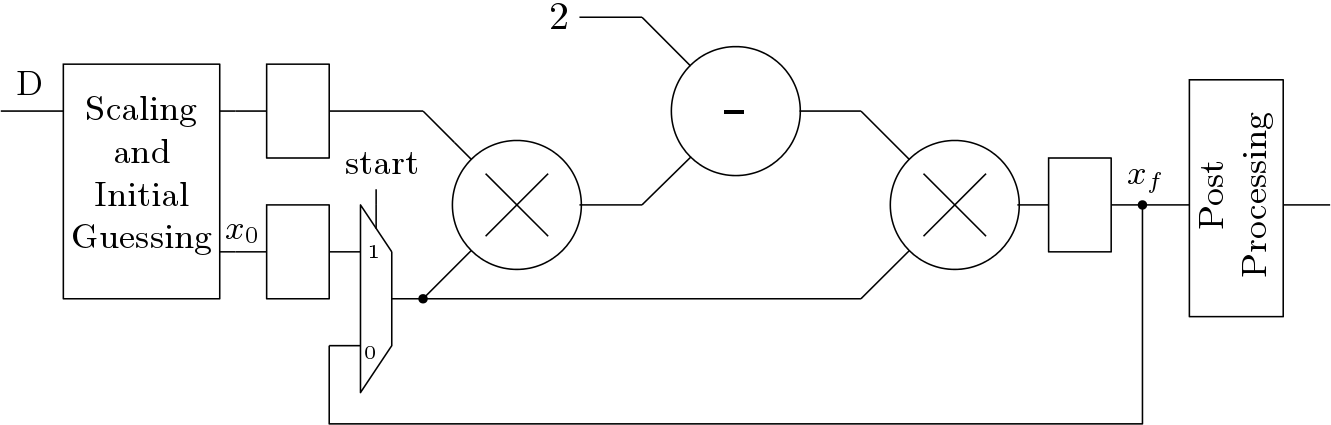
Newton-Raphson Based Reciprocal Computation
Click here to download the Verilog Code
