Fast Multiplication

The fast multiplication can be achieved in three general ways.

1. The sequential multipliers sequentially generates the partial products and adds them with the previously stored partial products.
2. In the second method, high speed parallel multipliers generate the partial products in parallel and adds them by a fast multi-operand adder.
3. The third method corresponds to use of array of identical blocks that generates and adds the partial products simultaneously.

The sequential multipliers have to work at high frequency and thus consumes high power. The performance of the parallel multipliers depends on the performance of multi-operand adder and also on the optimal number of partial products. The third method is actually the array multiplier having high hardware complexity. An obvious method to design a fast multiplier is to reduce the partial products and then applying fast addition methods. Here we will first discuss the methods to reduce the partial products and then fast multi-operand addition techniques will be discussed. A steps of designing a fast multiplier is shown in Figure 1. All the steps are described below in details.

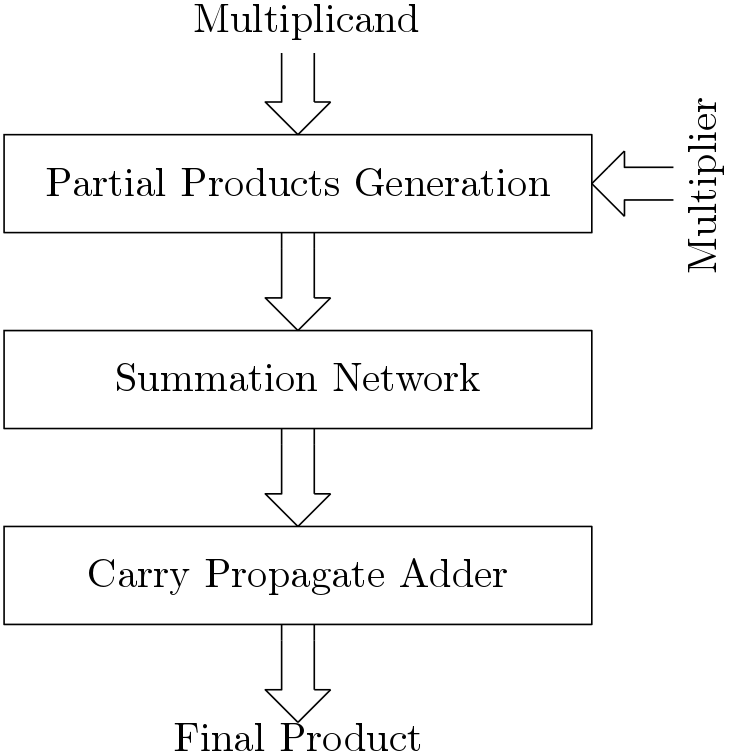
Partial Product Generation and Reduction

The first step towards designing a fast multiplier is generation of partial products. The performance of a fast multiplier depends on generating fewer partial products. The lower number of partial products means high speed of multiplication. There are two methods to reduce the number of partial products which are

1. Booth’s multiplication algorithm
2. Implementing larger multiplier by smaller ones.

Accumulation of Partial Products

The optimum number of partial products can be obtained by applying any of the algorithms mentioned above. The next job in designing a fast multiplier is to accumulate these partial products by a fast accumulating circuit. In this section, all the techniques involved in fast accumulation of partial products is discussed. The techniques are categorized as

1. Accumulation of Partial Products for Unsigned Numbers.
2. Accumulation of Partial Products for Signed Numbers.
3. Alternative methods of partial products accumulation.

Carry Propagate Adder

After applying the above techniques for accumulating the partial products, a carry propagation stage is required to produce the final result of multiplication. This stage is similar to the last stage of a array multiplier. Though we need to avoid the carry propagation stage but at least one carry propagating stage will be required.

Multiplier Designs

1. Sequential Multiplier : Sequential Multiplier is an old method to multiply two binary numbers. But it is also relevant in many architectures and it is the base of many newly developed multiplication techniques. Booth’s algorithm can be designed to execute sequentially to compute fast multiplication.
2. Unsigned Array Multiplier : Array multiplier is very popular for multiplication of binary numbers. Array multiplier resembles the pen and paper method of multiplication process. Here an unsigned multiplier for two 4-bits are shown.
3. Booth’s Array Multiplier: Booth’s algorithm is a powerful technique to achieve fast multiplication. Booth’s algorithm can be employed either sequentially or with the help of fast addition methods or in the form of array multiplication. In this tutorial, Booth’s Radix-4 algorithm is used to form an architecture to multiply two 6-bit numbers in the form of array multiplier.
4. Wallace and Dedda Multiplier Design : Wallace and Dedda together gave some suggestions to achieve fast multiplication with limited resources. They applied almost similar techniques by using HAs and FAs as basic elements.
5. Dedicated Square Block: In applications where square operation required, we need not use a multiplier. A dedicated square block is hardware efficient than a multiplier. The reduction of hardware is shown in this tutorial.
6. Signed Array Multiplier: In real time application, data can be signed and unsigned. Thus a multiplier should support both signed and unsigned operands. Thus here a tutorial on 4-bit signed array multiplier is given.
7. Multiplication using Look Up Tables: This also an simple but effective way to perform multiplication. Some times when serial multiplication is required, this technique proves very handy.

+4

0