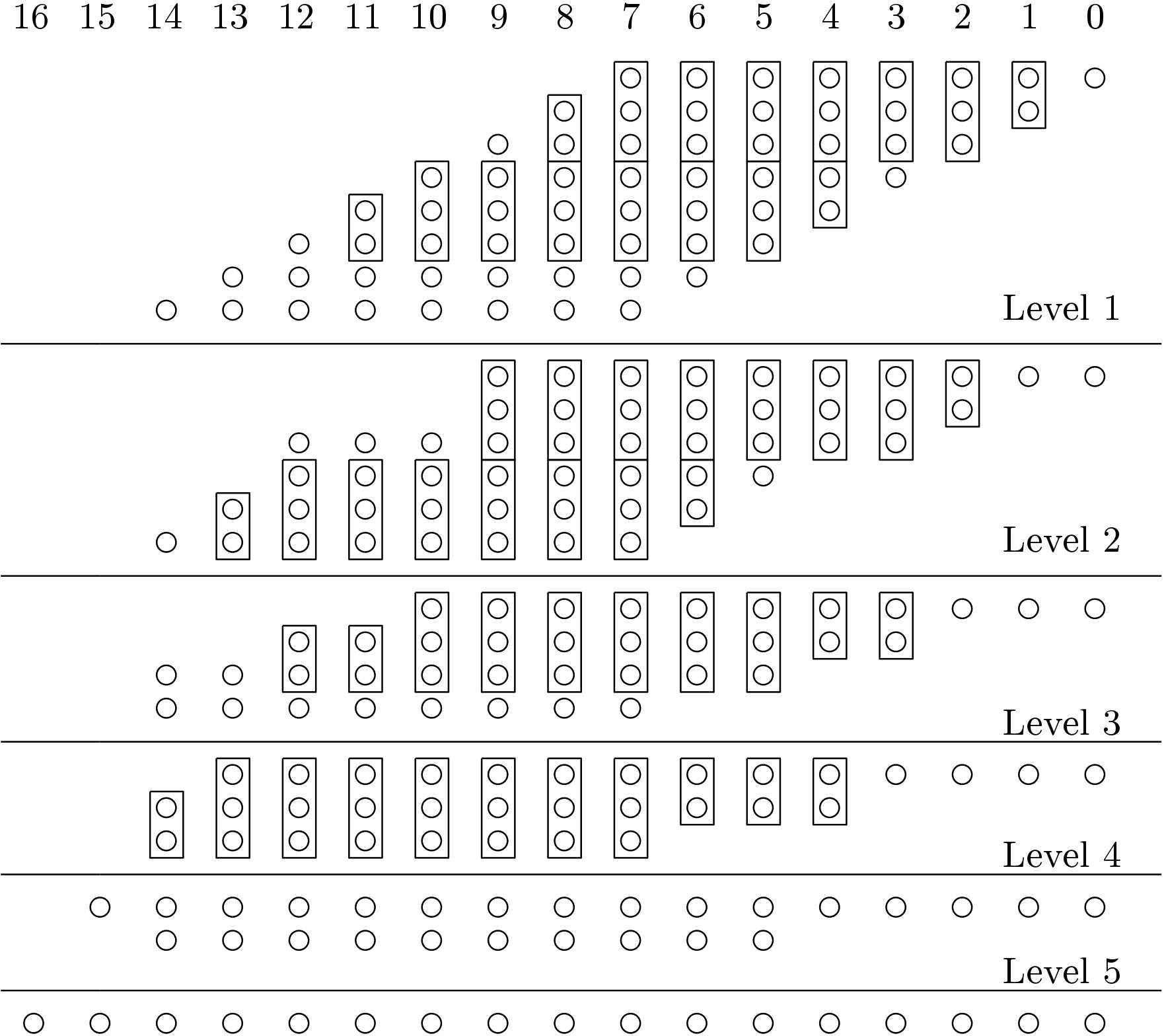
Chris Wallace in 1964 gave some suggestions on fast multiplication. In order to achieve high speed without consuming extra hardware he suggested techniques. He proposes to use the basic HAs and FAs as basic elements for operand reduction. He applied operand reduction in parallel layers and achieve better speed. The steps are
- Obtain the partial products and form the matrix.
- Apply the HAs and FAs to reduce the operands. Try to reduce the operands as much as possible in parallel.
- Apply carry propagating adder to generate the final product.
The flow of the Wallace tree multiplier is shown below in Figure 1 for 8-bit numbers. There are total 5 layers of addition involved. Total 16 numbers of HAs are consumed and total 47 number of FAs are consumed.
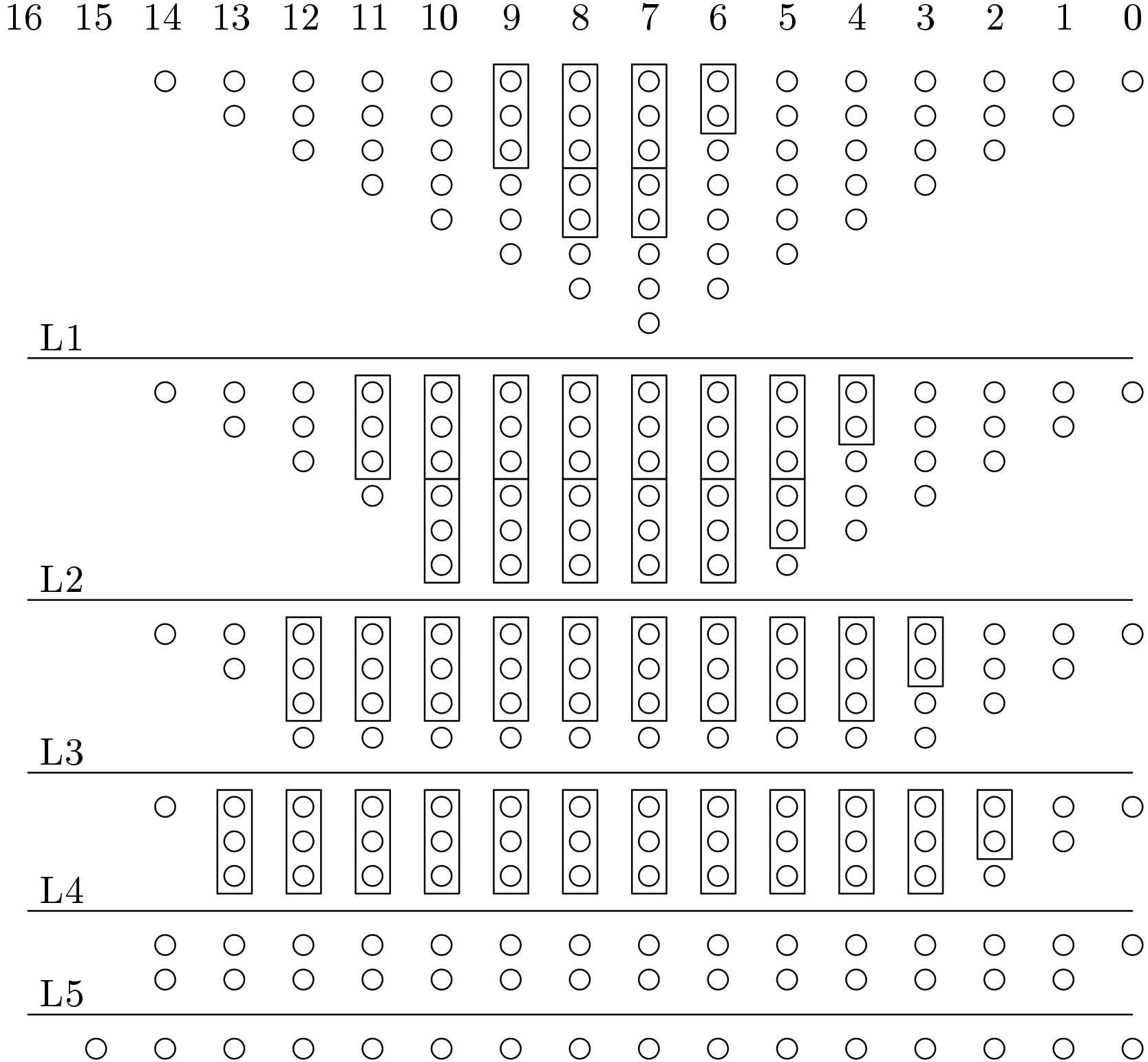
Luigi Dadda in 1965 also gave some suggestions on fast multiplication. He proposes some similar suggestions to achieve better speed. Dedda targets to reduce the operands in a particular manner so as to consume minimum number of basic elements. He achieves slightly better speed than the Wallace multiplier but consumes less hardware. The steps are
- Obtain the partial products and form the matrix. Rearrange the matrix in the form of a tree.
- Apply the HAs and FAs to reduce the operands. Try to reduce the operands as much as possible in parallel. Keep the height of length taking value from the set {2, 3, 4, 6,…..}.
- Apply carry propagating adder to generate the final product.
The flow of the Dedda tree multiplier is shown below in Figure 2 for 8-bit numbers. There are total 5 layers of addition involved. Total 8 numbers of HAs are consumed and total 48 number of FAs are consumed.
Click here to download the code for Wallace Multiplier.
Click here to download the code for Dedda Multiplier.
