Multiplier is a major block in designing digital systems. Several algorithms are reported in literature to implement fast multipliers. VEDIC multiplication algorithm is another option to implement an efficient multiplier. This work discuses the VEDIC multiplier. There are 3 methods to implement multiplication in VEDIC mathematics. Out of three, only one method is generic method which can be applied to all cases whereas other two are for special cases. Main algorithm of Vedic multiplication is Urdhva Triyakbhyam. It is a general multiplication formula applicable to all cases of multiplication. It literally means Vertically and Crosswise.
The multiplication of two operands using VEDIC multiplier is achieved by multiplication by Vertically and Crosswise and then adding all the results. This multiplication algorithm can be understood using two operands 46 and 33. The operand 33 can be represented as 33 = (3×10 + 3) and 46 can be represented as 46 = (4×10 + 6). The multiplication (46×33) can be represented as (3×6 + 40×3 + 30×6 + 30×40). This multiplication is shown in Figure 1

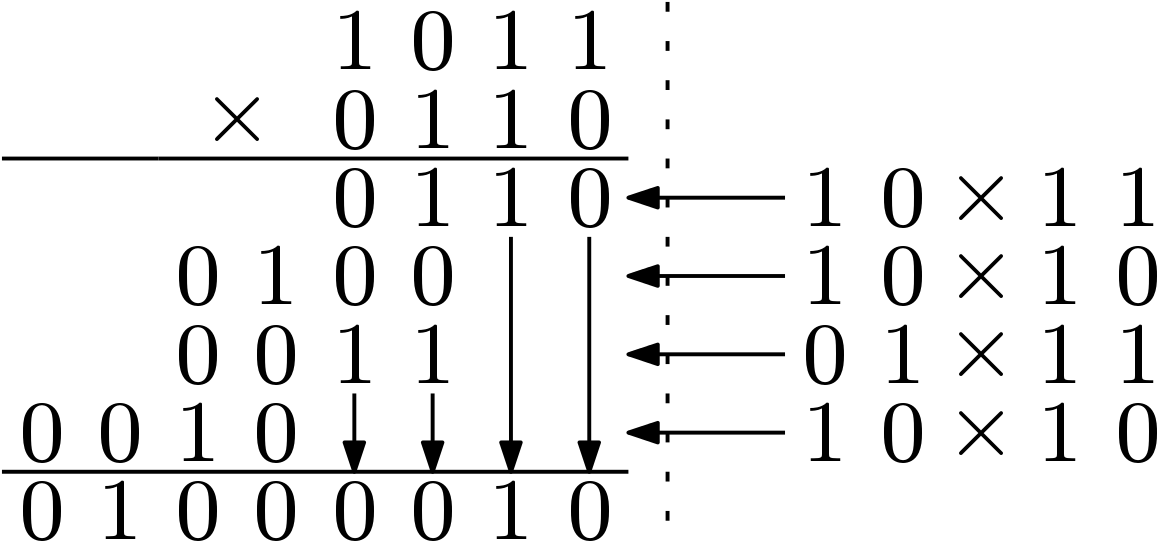
Similar way, this multiplication algorithm can be adopted to implement faster binary multiplier. A 4-bit binary multiplication is shown below in Figure 2
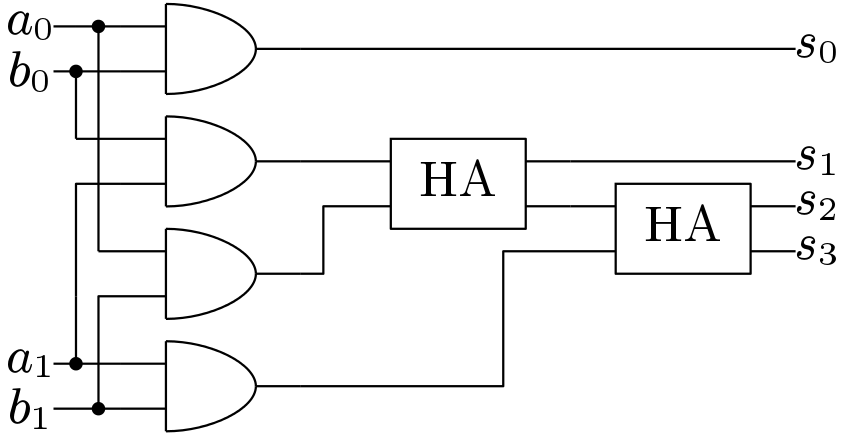
VEDIC multiplier is a good alternative to the other fast multiplicative algorithms. VEDIC multipliers reduces hardware as well as the delay compared to other algorithms. A 2-bit multiplier is shown in Figure 3. This circuit uses just two HA blocks and four AND gates.
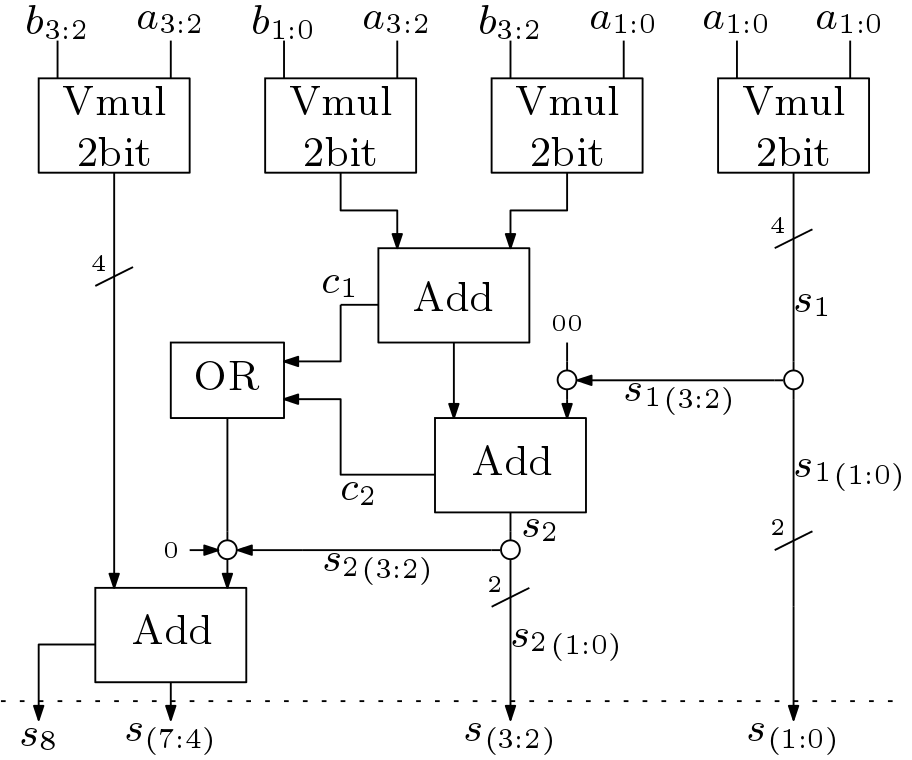
VEDIC multiplier for 4-bit data width is shown in Figure 4. This structure is achieved using four 2-bit multipliers. Here three Add blocks are used. These blocks can be implemented using high speed adders like conditional sum adder, carry look ahead adder or carry select adder as shown in the post fast addition. In this Figure the circles represent the concatenation block. For example, the two bits from the wire ![]() are connected to the output directly.
are connected to the output directly.

thank you sir!!! great work 🙂