In our previous tutorial, we have discussed about Cholesky decomposition which is a very important matrix factorization to solve a linear equation. But this technique has some drawbacks which are also discussed in the same tutorial. In this tutorial, we will discuss about modified Cholesky Decomposition which is an alternative version of Cholesky decomposition. This technique alleviates the requirement of square root operation which is a complex arithmetic operation. Similar to the Cholesky decomposition, the co-efficient matrix ![]() has to be a symmetric positive definite matrix in this technique. But in general, the co-efficient matrix can be rectangular or square and it may not be symmetric. Thus, traditional linear equation is not suitable for modified Cholesky based techniques. In order to solve the linear equations by modified Cholesky based technique, the traditional linear equation is multiplied by
has to be a symmetric positive definite matrix in this technique. But in general, the co-efficient matrix can be rectangular or square and it may not be symmetric. Thus, traditional linear equation is not suitable for modified Cholesky based techniques. In order to solve the linear equations by modified Cholesky based technique, the traditional linear equation is multiplied by ![]() in both sides. New equation becomes.
in both sides. New equation becomes.
(1) 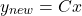
where ![]() and
and ![]() . Now, matrix
. Now, matrix ![]() is symmetric positive definite of size
is symmetric positive definite of size ![]() . This matrix can be factored using modified Cholesky decomposition as
. This matrix can be factored using modified Cholesky decomposition as
(2) 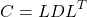
Here, ![]() is a lower triangular matrix having all the diagonal elements equal to 1 and
is a lower triangular matrix having all the diagonal elements equal to 1 and ![]() is a diagonal matrix with off-diagonal elements equal to 0. This decomposition technique also known as LDL decomposition. Modified Cholesky decomposition is said to be efficient than both Cholesky and LU decomposition. Inverse of the matrix
is a diagonal matrix with off-diagonal elements equal to 0. This decomposition technique also known as LDL decomposition. Modified Cholesky decomposition is said to be efficient than both Cholesky and LU decomposition. Inverse of the matrix ![]() can be computed as
can be computed as
(3) 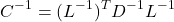
The elements of the ![]() matrix are computed by the following equations.
matrix are computed by the following equations.
(4) 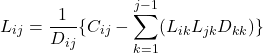
Here, variable ![]() can be varied from 1 to
can be varied from 1 to ![]() and variable
and variable ![]() can be varied from
can be varied from ![]() to
to ![]() . The following equation computes the elements of the matrix
. The following equation computes the elements of the matrix ![]()
(5) 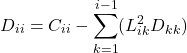
In order to calculate the inverse of the matrix ![]() , inverse of both the matrix
, inverse of both the matrix ![]() and
and ![]() should be computed. The inverse of the matrix
should be computed. The inverse of the matrix ![]() is computed by the following equation.
is computed by the following equation.
(6) 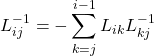
Matrix ![]() is a diagonal matrix where all the off-diagonal elements are zero. Thus, computation of reciprocal of the diagonal elements are enough. This can be done by a dedicated reciprocal unit.
is a diagonal matrix where all the off-diagonal elements are zero. Thus, computation of reciprocal of the diagonal elements are enough. This can be done by a dedicated reciprocal unit.
Comparison with Cholesky Factorization: Modified Cholesky Factorization is more popular than Cholesky Factorization. This is because, Cholesky Factorization involves square root operation as well as reciprocal operation to evaluate the elements of L and inverse of L respectively. Both these operations have higher computational complexity. In modified Cholesky decomposition, only reciprocal operation is required.
MATLAB code for Modified Cholesky (5819 downloads )