Scalar-Vector multiplication is a very important arithmetic operation in implementing signal or image processing algorithms. In this tutorial, we will discuss the hardware for multiplication between a 6X3 Matrix (A) and a 3X1 Matrix (B) and the result is a 6X1 column vector (C). This multiplication is shown below in Figure 1.
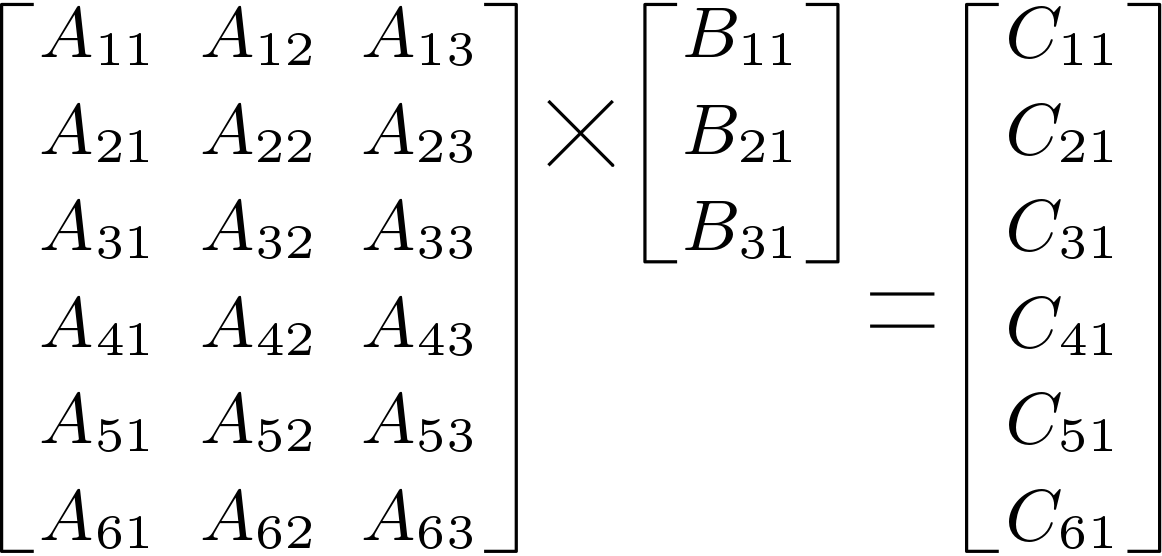
This multiplication can be achieved in two ways, either by vector-vector multiplication or by scalar-vector multiplication. In scalar-vector based multiplication, one column of matrix and one element of column vector B is fed to the computing processor. This multiplication result is accumulated with the multiplication of 2nd column of A and second element of B. Thus the matrix and vector multiplication is achieved through scalar-vector multiplication and accumulation. The multiplication between A and B can be expressed as
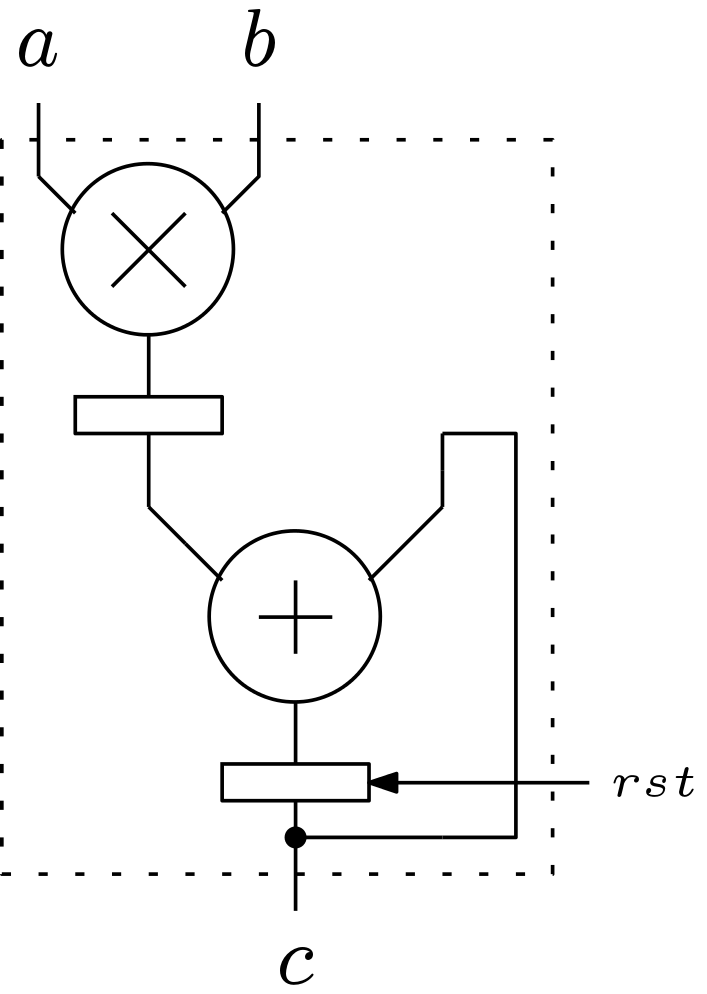
The computing unit is designed using a basic Multiply and ACumulate (MAC) unit. This unit multiplies two elements and accumulate. The schematic of this MAC unit is shown below in Figure 2.
The overall computing unit is shown below in Figure 3.
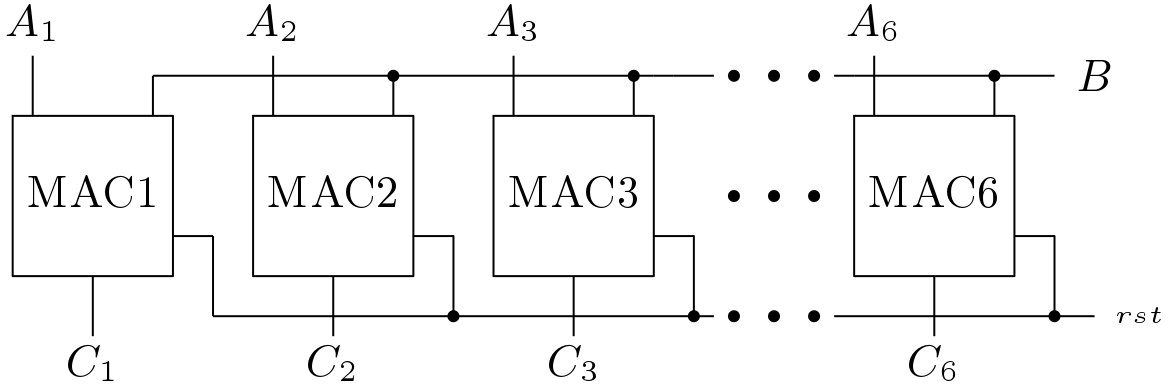
There are six MAC blocks are used. The latency of the MAC block is two clock cycles. But after four clock cycles the vector C is computed. The reset (rst) input is very important here. The register after the adder in the MAC block should be cleared before the multiplication and before starting another multiplication. The timing diagram for the MAC block computation is shown below in Figure 4.
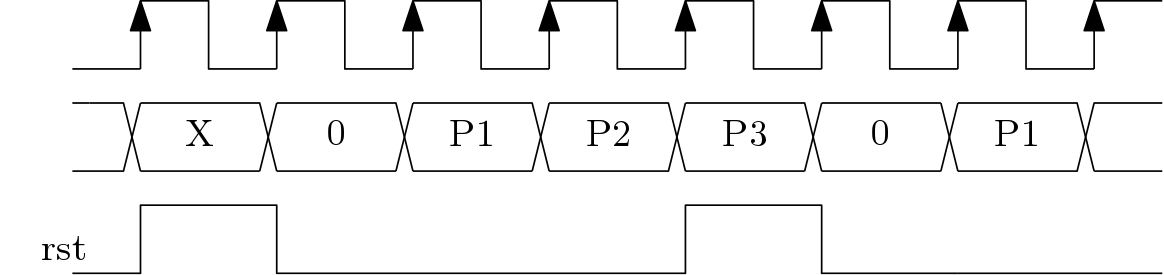
Here P is the output of the MAC block. P1 is the first multiplication output, P2 is the first accumulation output and the P3 is the final output. The computing unit consumes six multipliers and six adders.
