Restoring Algorithm for Square Root - Digital System Design

The Restoring algorithm for square root is similar to the Restoring division algorithm. Let X is the positive radicand and its square root is represented as $Q_n = 0.{q_1}{q_2}{q_3} .... q_n$ , when n is the total number of iterations. The bits of Q are generated in n number of steps, one bit per iteration. The $Q_i$ is expressed as

$Q_i = \sum_{k=0}^{i}q_k2^{-k}$

The Restoring algorithm for square root operation can be considered as division operation with varying divisor. The Restoring algorithm for square root computation is shown below in Fig. 1. An example of the square root computation of the radicand X = 0.1011 is shown below in Fig. 2. The result is Q = 0.1101. The value of n is 4 here.

Fig. 1: Restoring Algorithm for Square Root

Fig. 2: An Example of Restoring Algorithm Based Square Root

The hardware implementation of Restoring algorithm based square root computation is shown in Fig. 3. Here 8-bit operand X is taken as input and thus Q is of 4-bit. Here total 17 sub blocks (SBs) are used and the logic diagram of the SB is given also in Fig. 3. A full subtractor is used to perform the subtraction operation. A mux is used to perform the restoring operation. Whenever the sel signal is 1, SB restores input a to the output.

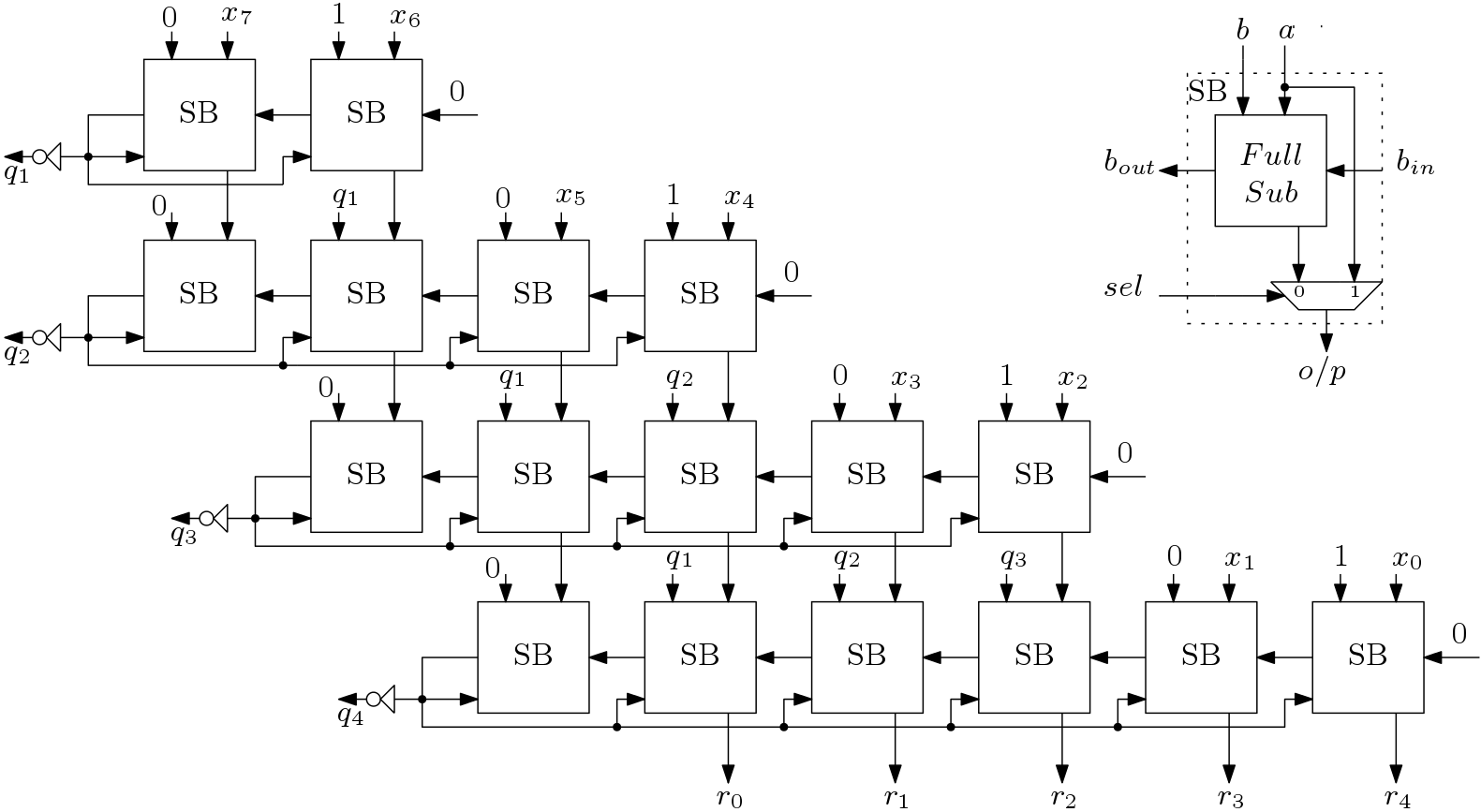
Fig. 3: Implementation of Restoring Algorithm Based Square Root

Click here to download the Verilog Code

Related Posts