Floating Point Addition and Subtraction

Compared to a fixed point addition and subtraction, a floating point addition and subtraction is more complex and hardware consuming. This is because exponent field is not present in case of fixed point arithmetic. A floating point addition of two numbers $a$ and $b$ can be expressed as

${S_a.M_a.2^{E_a}} + {S_b.M_b.2^{E_b}} = S.2^{E_b}({M_a} + {M^*_b})$

Here, it is considered that $E_a>E_b$ . In this case, ${M^*_b}$ represents the right shifted version of $M_b$ by $|E_a-E_b|$ bits. Similar operation is carried out for $E_a<E_b$ . Thus floating point addition and subtraction is not as simple as fixed point addition and subtraction.

The major steps for a floating point addition and subtraction are

Extract the sign of the result from the two sign bits.
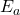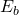Subtract the two exponents $E_a$ and $E_b$ . Find the absolute value of the exponent difference ( 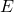$E$ ) and choose the exponent of the greater number.
Shift the mantissa of the lesser number by 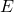$E$ bits Considering the hidden bits.
Execute addition or subtraction operation between the shifted version of the mantissa and the mantissa of the other number. Consider the hidden bits also.
Normalization for addition: In case of addition, if there is an carry generated then the result right shifted by 1-bit. This shift operation is reflected on exponent computation by an increment operation.
Normalization for subtraction: A normalization step is performed if there are leading zeros in case of subtraction operation. Depending on the leading zero count the obtained result is left shifted. Accordingly the exponent value is also decremented by the number of bits equal to the number of leading zeros.

Example: Floating Point Addition

Representation: The input operands are represented as 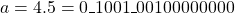$a = 4.5=0\_1001\_00100000000$ and $b = 3.75=0\_1000\_11100000000$
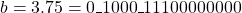
Sign extraction: As both the numbers are positive then sign of the output will be positive. Thus S = 0.
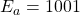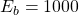Exponent subtraction: $E_a = 1001$ and $E_b = 1000$ . Thus result of the subtraction is E = 0001.
Shifting of mantissa of lesser number: The mantissa 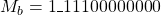$M_b = 1\_11100000000$ is shifted by 1 bit right and the result is $M_b = 0\_11110000000$ .
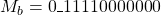Result of the mantissa addition is 000010000000 and generates a carry. This means the result is greater than 1.
The output of the adder is right shifted and the exponent value is incremented to get the correct results. The new mantissa value is now 00001000000 choosing the last 11-bits from the LSB and exponent is 1010.
The final result is 0_1010_00001000000 which is equivalent to 8.25 in decimal.

Example: Floating Point Subtraction

Representation: The input operands are represented as 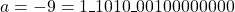$a = -9=1\_1010\_00100000000$ and $b = 3.9375=0\_1000\_11111000000$ .
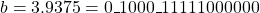Sign extraction: As sign of $a$ is negative and $a$ is greater thus S = 1.
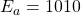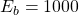Exponent subtraction: $E_a = 1010$ and $E_b = 1000$ . Thus result of the subtraction is $E = 0010$ .
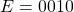Shifting of mantissa of lesser number: The mantissa 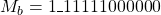$M_b = 1\_11111000000$ is shifted by 2 bit right and the result is $M_b = 0\_00111110000$ .
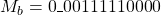Result of the mantissa subtraction is 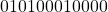$010100010000$ . This leading zero indicates that the result is lesser than 1.
The output of the adder is left shifted by 1 bit as there is one leading zero and the exponent value is decremented by 1-bit to get the correct results. The new mantissa value is now 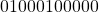$01000100000$ choosing the last 11-bits from the LSB and exponent is 1001.
The final result is 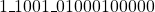$1\_1001\_01000100000$ which is equivalent to -5.0625 in decimal.

A simple architecture of a floating point adder is shown below in Figure 1.

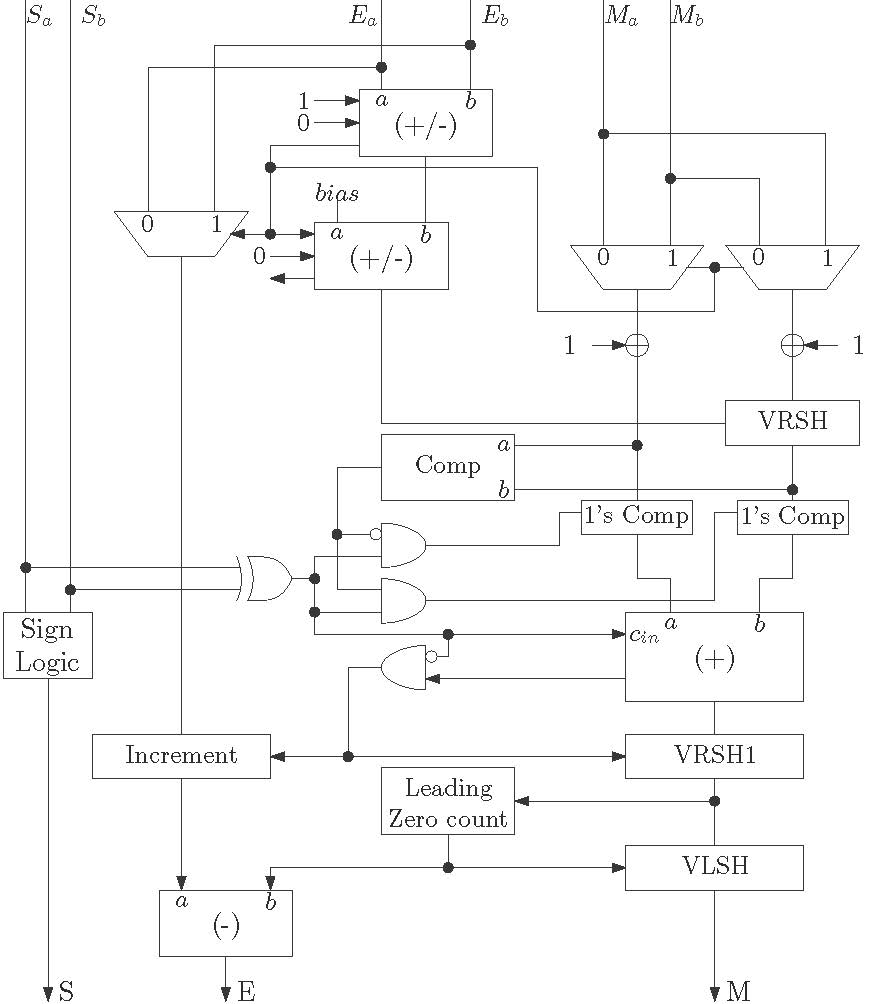
Figure 1: A basic scheme for 16-bit floating point addition.

In this architecture, three 4-bit adders are used for computing the exponent and a 12-bit adder is used for adding or subtracting the mantissa part. Two MUXes before the mantissa computation path selects the selects the mantissa of the lower number for shifting. The shift operation is carried out by a VRSH block. This block shifts the mantissa according to the exponent difference. The addition or subtraction is done by 2’s compliment method. Thus a comparator is used to detect the smaller mantissa for inversion.

The leading zero counter is for normalizing the result in case of subtraction operation when the mantissa part contains the leading zeros. This block has no meaning in case of addition operation. The VLSH block is a variable left shifter like VRSH block.

The hardware complexity of the floating point addition and subtraction block is much higher than the fixed point adder subtractor block. This due to the fact that floating point includes exponent field and also normalization is required if the result is fractional.

+22

-3

Related Posts