Square of a number can also be computed using VEDIC arithmetic formulas. Square computation is generally faster and hardware efficient than the complete multipliers. Similarly a VEDIC square block is hardware efficient than the multiplier block. Square of an operand is computed using the Dwandwa Yoga or Duplex method.
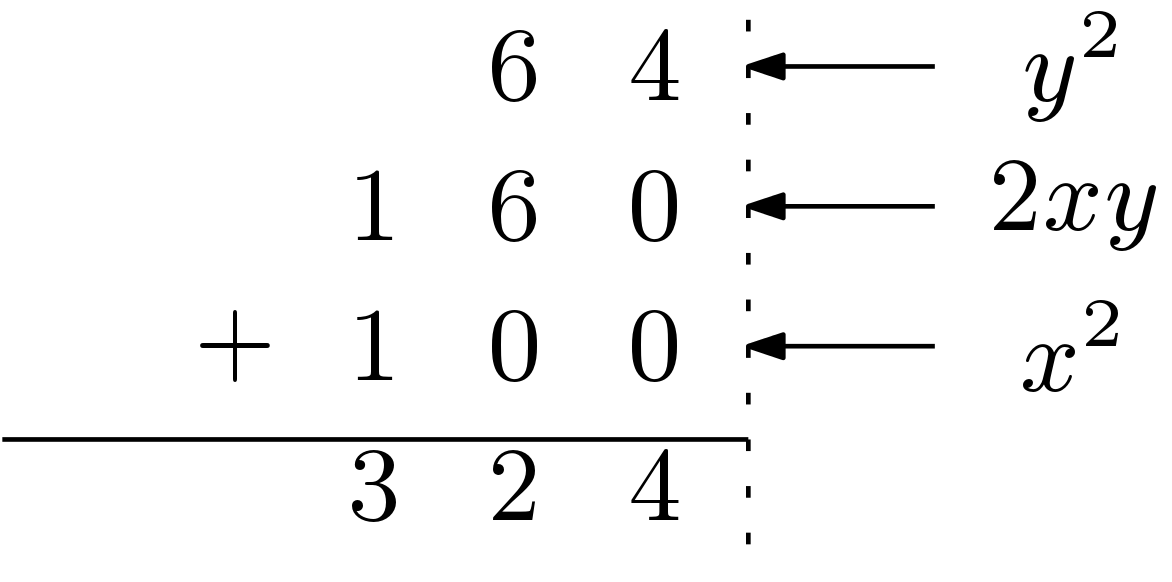
Any number can be represented as (x + y) and in this method, square of this number can be computed as
This can be shown with an example. Lets the operand is 18 and 18 can be represented as (1×10 + 8). Thus the square of this number using duplex square method is shown in Figure 1.
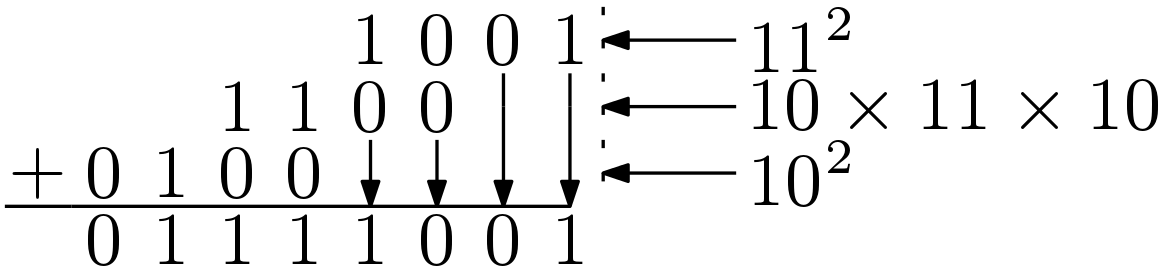
Similarly, duplex square method can be applied to the Binary numbers as well. This is shown in Figure 2 by taking ‘1011’ as example.
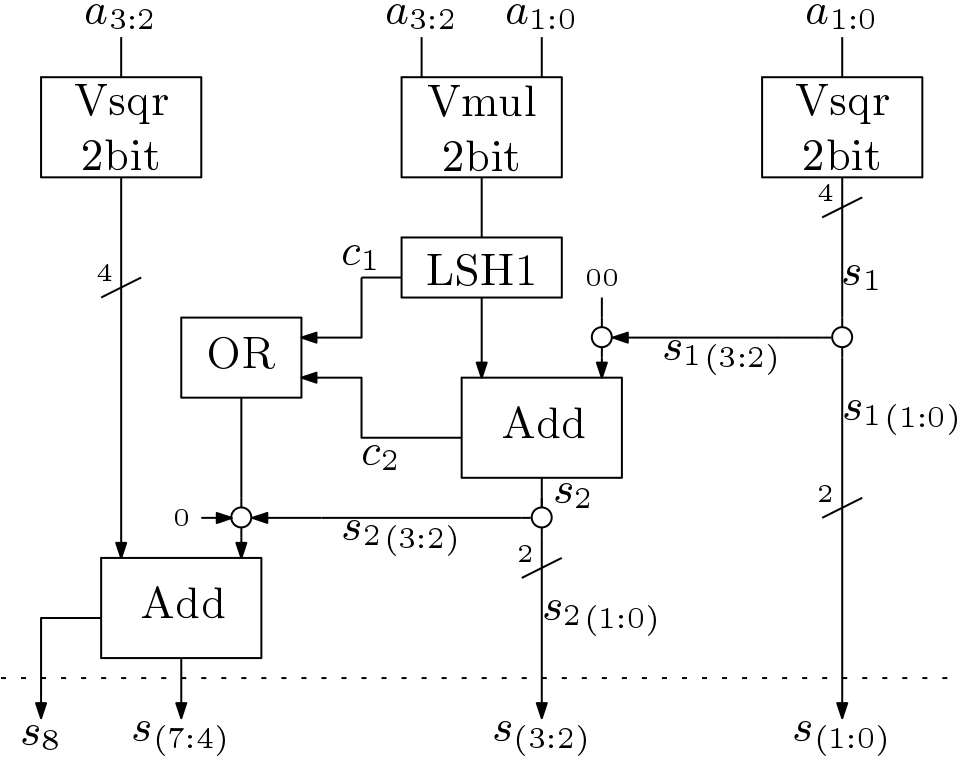
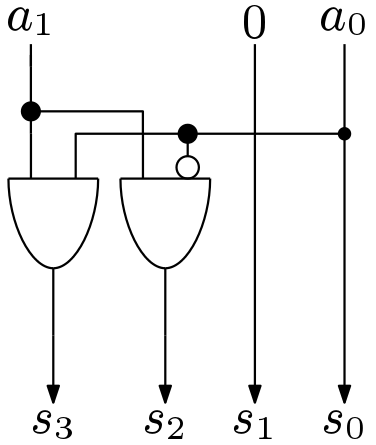
As discussed earlier that, squaring operation is easier than multiplication. This will be clearer by seeing the architecture. The 2-bit duplex square block architecture is shown in Figure 3.
This block is used to develop the 4-bit duplex square block. The architecture of 4-bit square block is shown in Figure 4. Here, two 2-bit square block and one 2-bit multiplier block are used. The LSH1 block is used for left shifting for 1-bit. This shifting is wired shifting as discussed in the post combinational circuits. Here, two Add blocks are used in comparison to the three blocks in case multiplier. These blocks can be implemented using high speed adders like conditional sum adder, carry look ahead adder or carry select adder as shown in the post fast addition. In this Figure the circles represent the concatenation block.