Apart from the multiplication and square, finding cube of a number is an another important operation in signal processing. The cube of a number can be computed using Anurupya Sutra which is the subsutra of Ekadhikena Purvena. VEDIC Cube architecture is efficient in terms of hardware and also in terms of delay.
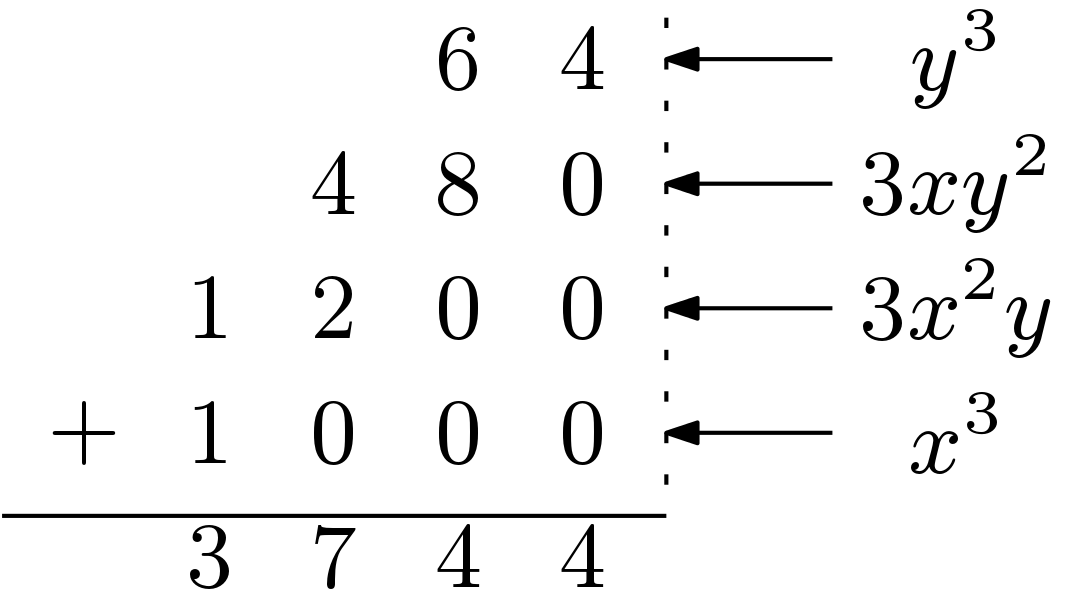
Cube of a number (
) can be computed easily using the VEDIC sutras. First express the numbers (z) as sum of two parts as (z = x + y). Then the cube of that number can be computed as
This operation is explained below in Figure 1 with a proper example
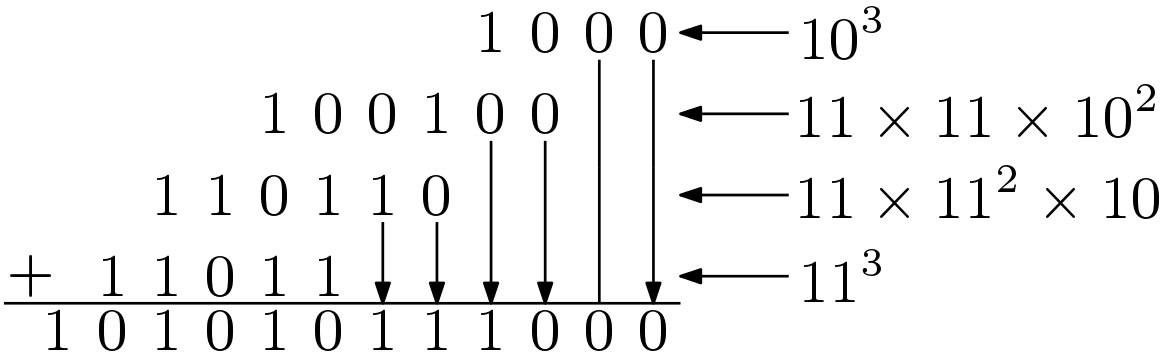
This method can be easily adopted for the binary numbers. VEDIC cube for 4-bit binary number is shown in Figure 2 for z = ‘1110’
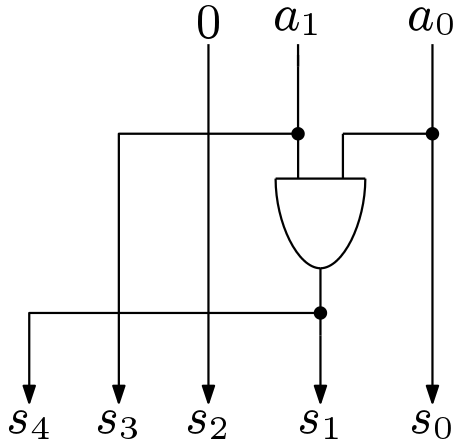
In the computation of cube, several other operations are involved. These are square, multiplication and lower order cubes. The architecture of these blocks are discussed in earlier posts. Here the cube architectures are discussed. The 2-bit VEDIC cube architecture is shown in Figure 3. This is optimized and simple block.
The 4-bit VEDIC cube architecture is shown in Figure 4.
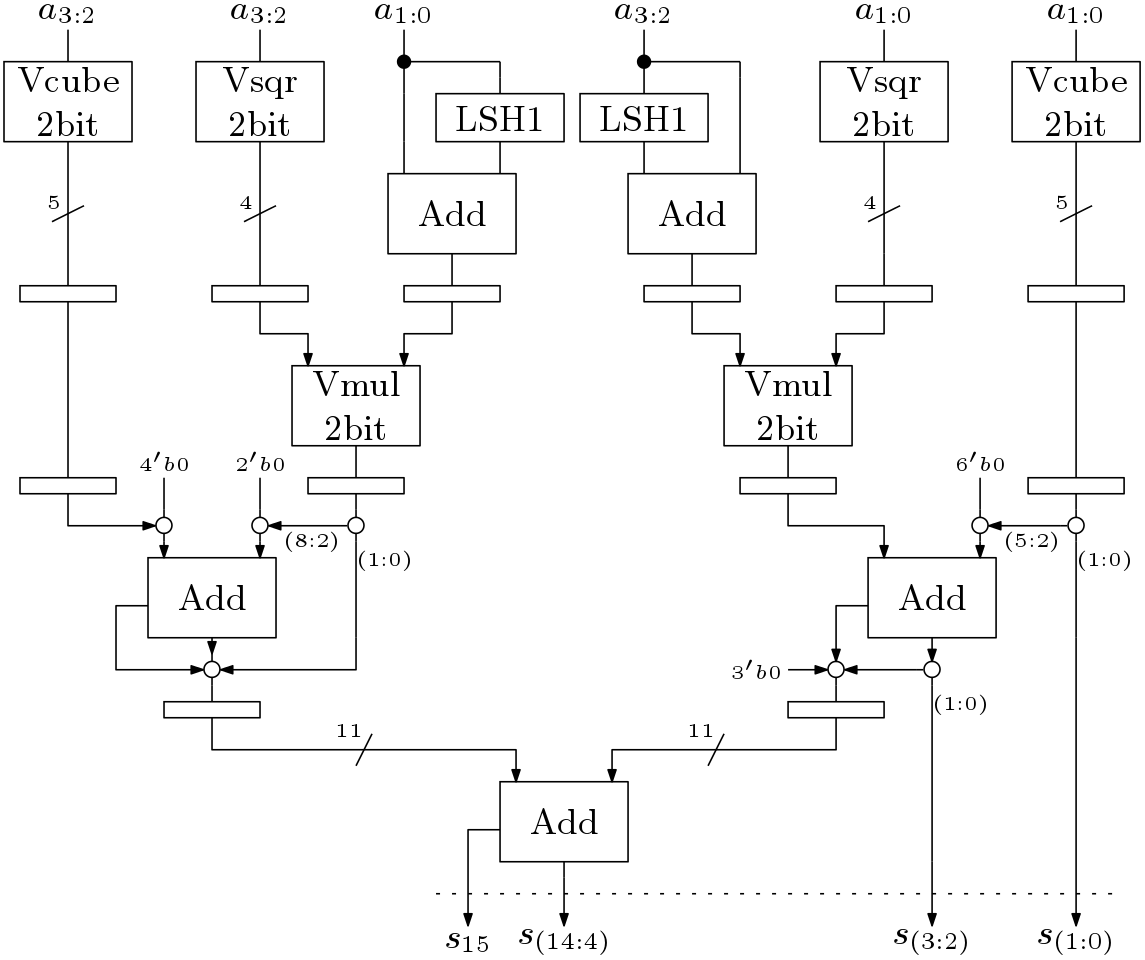
In the above Figure, starting from the left side the operations computed are 
, 
, 
,
, 
and 
. All these operations are computed in parallel. This is the main advantage of this method. Multiplication by ‘3’ is obtained by first multiplying by 2 and then adding the input number. The block LSH1 multiplies a number by 2 using wired left shifting. and are multiplied to obtain 
. Similarly, 
is computed. Then,
and
are computed parallel. The results are added together at the last stage. The pipeline registers are also shown in suitable places. The circles are placed for concatenation operation. The Add blocks can be implemented using high speed adders like conditional sum adder, carry look ahead adder or carry select adder as shown in the post fast addition.
very well explained !!