Exponential function is very important to evaluate activation functions (Sigmoid, hyperbolic tangent, SoftMax etc.) used in machine learning (ML) algorithms. Thus, efficient hardware implementation of exponential function very important. In this post, we have discussed detailed FPGA Implementation of Taylor Series Based Exponential function.
Many techniques are reported in literature to compute exponential function. Taylor series expansion is one of the popular technique to approximate exponential function. Taylor series expansion of exponential function for positive value of x is
(1) 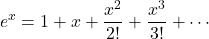
Taylor series expansion of exponential function for negative value of x is
(2) 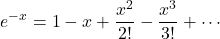
Exponential function can be approximated by taking 4 terms of Taylor series only. The above equations can be evaluated by serial computation step by step. Taking only 4 terms, the above equation for positive exponential can be written as
(3) 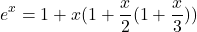
Similarly, the negative exponential can be written as
(4) 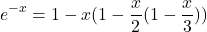
The range of exponential function is an issue in implementing the activation functions in ML algos. All the algorithms for exponential calculates for input range of -1 to 1. Beyond this range it is not possible to compute exponential function. Thus adjusting input data range is important. But in some applications it is required to extend the range of exponential function. Range can be extended by expressing the input data as
(5) 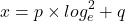
Thus q will in the range -1 to 1 and the exponential block will find the exponential of q. At the output exponential of x is computed as
(6) 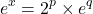
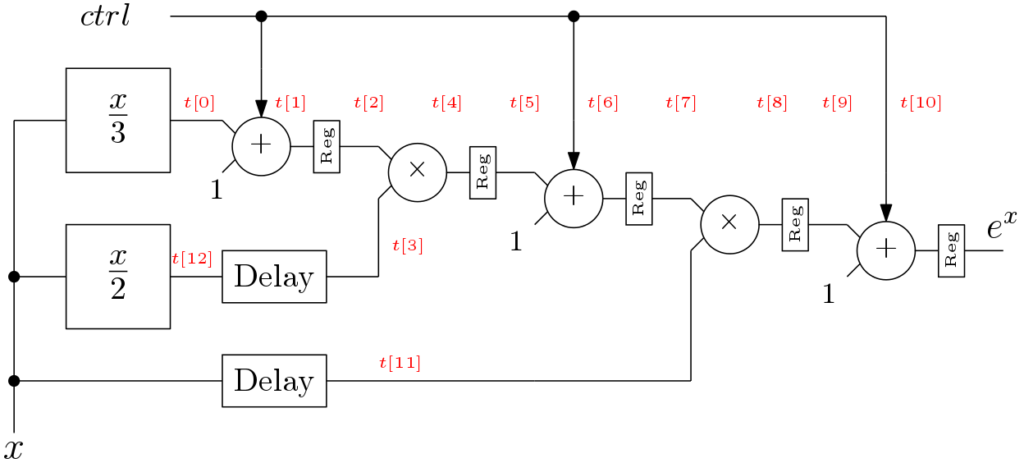
The exponential block architecture should be designed such a way that it can compute exponential for both positive and negative values. A parralel and pipelined architecture is designed here and shown in Figure 1. The computation of x/3 is performed by a scale block. More about the scale block architecture is given in our earlier post. The architecture uses precision of 9 bits. Means 9 bits are used for fractional part. Total 12 bits are enough to accommodate the whole range of exponential function when input range is from -1 to 1. An ctrl signal is used to control the operation of adder/subtracters. If the ctrl signal is high, then subtraction is performed. The architecture has total latency of 7 clock cycles and achieves more than 200 MHz frequency.
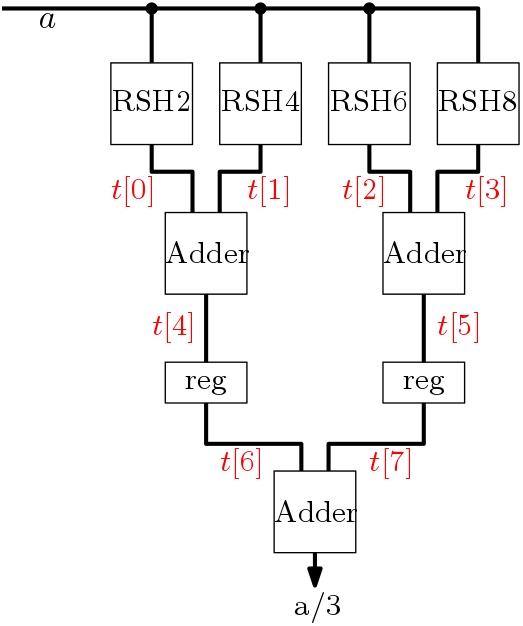
The scale block architecture to divide input data by 3 is shown in Figure 2. The red colored texts are intermediate wires shown
The architecture has acceptable accuracy. The error is introduced is due to avoidance of few terms on Taylor series and having precision of 9 bits. The simulation for FPGA Implementation of Taylor Series Based Exponential is shown below

The Verilog code can be found here
Verilog Code for FPGA Implementation of Taylor Series Based Exponential (2458 downloads )