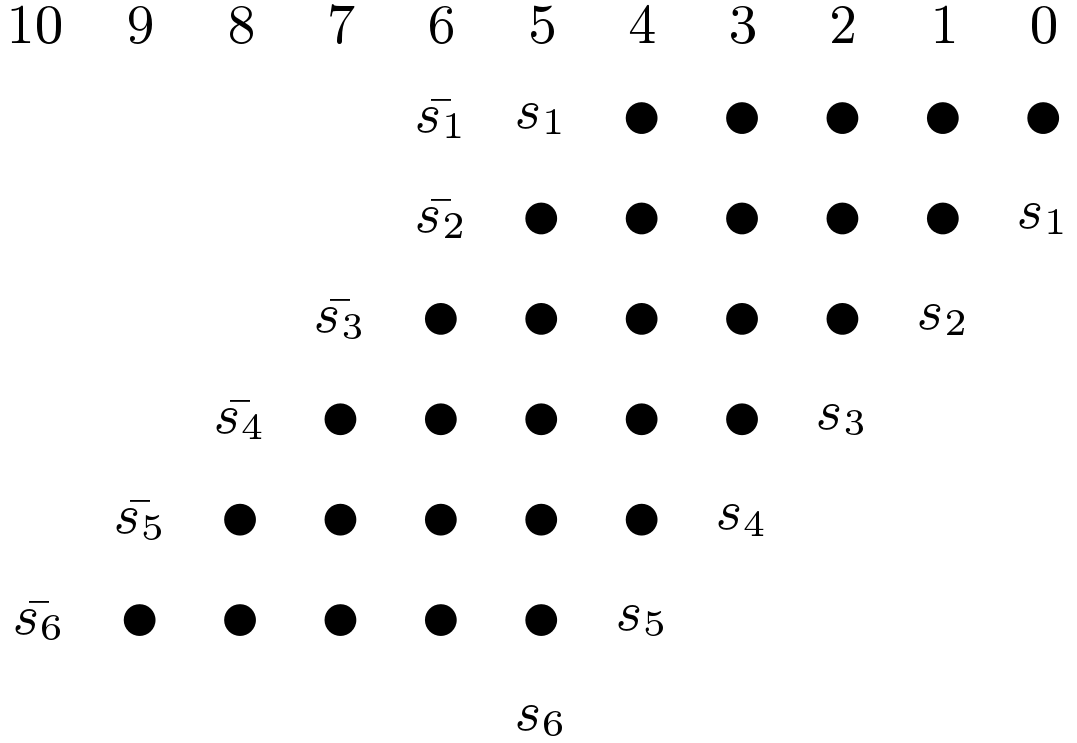
Accumulation of Partial Products for Signed Numbers

Earlier we have discussed how the partial products for a unsigned multiplier can be accumulated using suitable organization and consuming minimum number of counters. In this section, accumulation will be done by considering negative partial products. If some of the partial products are negative numbers represented in two’s complement number system, then matrix of bits needs to changed. All the sign bits must be properly extended before addition. The extension of sign bit is shown in Figure 1 for 6-bit partial products. Here the filled circles are representing sign bits. This modification increases the hardware complexity and also the number of stages. If the two’s complement numbers are obtained by generating one’s complement then a carry must be added in the least significant bit. This will again increases the hardware complexity.

Figure 1: Extension of sign bit in case of signed partial products

A six bit partial product $z_5z_4z_3z_2z_1z_0$ represented in two’s complement can be represented using 11-bit as

$s\hspace{1pt}s\hspace{1pt}s\hspace{1pt}s\hspace{1pt}s\hspace{1pt}s\hspace{1pt}z_4z_3z_2z_1z_0$

whose value is

$-s.2^{10} + s.2^9 + s.2^8 + s.2^7 + s.2^6 + s.2^5 + z_4.2^4 + z_3.2^3 + z_2.2^2 + z_1.2^1+z_0.2^0$

can be replaced as

$0\hspace{1pt}0\hspace{1pt}0\hspace{1pt}0\hspace{1pt}0\hspace{1pt}(-s)\hspace{1pt}z_4z_3z_2z_1z_0$

since

$-s.2^{10} + s.(2^9 + 2^8 + 2^7 + 2^6 + 2^5) = -s.2^{10} + s.(2^{10} - 2^5) = -s.2^5$

To represent the value -s in column 5, the original sign digit s is complemented to obtain (1-s) and 1 is added. This way we get -s in the column 6 along with a carry of 1. This carry serves as the extra 1 to deal with the sign of the second partial product. This way sign bit of all the partial products are dealt with. This solution is shown in Figure 2. Here number of bits compared to the array in Figure 1 is reduced but the height is increased.

Figure 2: The modified array of signed partial products.

The disadvantage of the first solution is that its length is 7. Now, the 1 in the column 5 can be eliminated if the two sign bits $s_1$ and $s_2$ can be placed in the same column. This is possible as $(1-s_1)+(1-s_2) = 2-s_1-s_2$ . This 2 is carried out to the next column leaving $-s_1$ and $-s_2$ . The extra 1 in column 5 is no longer required. Placing the two sign bits in the same column is achieved by extending the sign bit $s_1$ bit in one position as shown in Figure 3.

Figure 3: Second scheme to modify the array of signed partial products.

If the negative partial products are obtained by first generating the one’s complement and then adding a carry at the least significant side then the arrangement can be made different. The extra carry at the LSB side is then must be added to the matrix. This solution is shown in Figure 4 where the filled circles represent the complements of the bits whenever $s_i=1$ . Here in this solution the height of the matrix is again 7 but for the unsigned case the last carry at the LSB side can be omitted.

Figure 4 : Modified array of signed partial products represented with one’s complement.

The accumulation of signed partial products can be explained using an example. Let us consider the multiplication of two 6-bit numbers using Booth’s Radix-4 algorithm as used in previous tutorial. The partial products can be written as shown in Table 1.

Table 1: An example of sign extension for Booth’s Radix-4 algorithm

Here two partial products are negative represented in two’s complement format. The above mentioned techniques can be applied to decrease the number of operands. The general technique to reduce the operands in case of Radix-4 Booth algorithm for signed partial products is shown in Table 2.

Table 2: General operand reduction scheme for signed partial products for Booth’s Radix-4 algorithm

The matrix of the operand bits of Table 1 is modified by applying the second technique as shown in Table 3.

Table 3: Modified array of signed partial products for example shown in Table 1.

-1

Related Posts