In the previous post FSM Design, we have discussed design of Mealy and Moore state machines using Verilog. State minimization is important if we want to reduce number of states in a complex FSM which has many redundant states. If the number of states are reduced then number of bits required for state assignment will get reduced. Thus less number of flip-flops will be required and so there is chance to reduce combinational or sequential blocks also. This is why it is important to reduce the number of states. In this post we will discuss different state minimization techniques for FSM.
Before going to discuss the state minimization techniques some definitions must be known. If input 
is applied to a state machine in 
and NS is 
then is a 
-successor of 
. Similarly, If input 
is applied to a state machine in and NS is 
then is a 
-successor of . These two successors are generally called as 
-successors. Here PS indicates present state and NS indicate next state of a state diagram.
Two states and can be called equivalent if the following conditions are satisfied
- The states 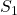and 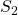should have same output for all the input sequences.
- Their 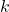-successors also obey the first criteria.
Some of the popular state minimization techniques are
- Row Equivalence Method
- Implication Chart Method
- State Partition Method
- Some Heuristic Methods
In this post only the first three techniques are discussed.
Performance of State Minimization Techniques
In this post, we have discussed three state minimization techniques for FSM . The row equivalence method is a basic method for state minimization. This method does not always lead to optimize number of states. The Implication chart method is a rigorous technique for state minimization. Though the chart preparation is difficult, it supports machine implementation. The partition based technique is simple but another rigorous method for state minimization. It is also machine realizable. Some of the heuristic methods based on K-map are also exists but they are more pen and paper methods.
State minimization techniques for FSM is a wonderful way to minimize the states and thus to reduce hardware elements. But there is not always a need to optimize a FSM. This is because sometimes minimization of states can lead to complex circuit. Sometimes state minimization reduce flip-flops but increase complexity in the combinational path. The state minimization is also difficult when there are don’t care conditions. It is even more difficult when don’t care conditions exists on output. Thus minimization algorithms must be carefully applied.
