Fixed Point Reciprocal Computation IP

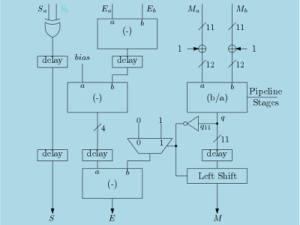
Sometimes in signal processing algorithms we have to find reciprocal or need to divide a fixed number by variable denominator. In such cases, we try to avoid the usage of complete divider as divider consumes lots of hardware resources. In order to compute reciprocal, many methods are available. Like, Newton Raphson iteration, Gold-Smith iteration, CORDIC algorithm etc. But if require a pipeline architecture for reciprocal then these methods are not suitable. Moreover these methods give errors in computing reciprocal. Thus we have designed a Fixed Point Reciprocal Computation IP which is based on partial division algorithm.

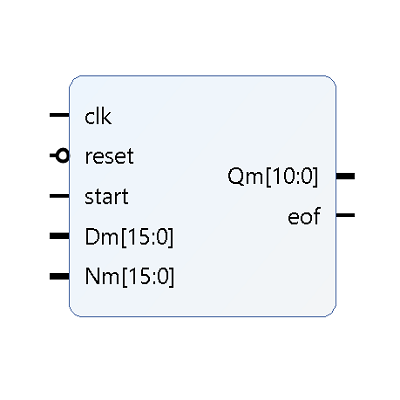
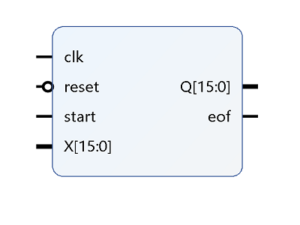
This IP is accurate, parallel, pipelined and have low latency compared to a complete divider. This IP can compute as well as can perform fixed division. It has 5 inputs which are clk, reset, start, Numerator (Nm), Denominator (Dm) and has two outputs which are Quotient (Qm) and eof. The start signal is synced with the input data and eof is synced with the output data. Here, numerator can be fixed to 1 if reciprocal is computed or can take any constant value.

This IP has three parameters which are data width (N), number of integer bits (L) and number of precision bits (M). The size of the output (Qm) is (L+M-1) bits. The minimum value of L is 1. Consider an example, Nm = 16’b000001_0000000000 for 10-bit precision. Now if Dm is equal to 16’b000001_0000000000 then the result is Qm = 0_1000000000. Integer and precision bits can be chosen as per requirement.

Fixed Point Reciprocal Computation IP is tested by implementing it on Xilinx XC7A35T-1FTG256 Artix 7 FPGA using logic analyzer. The FPGA performance for this IP is shown below

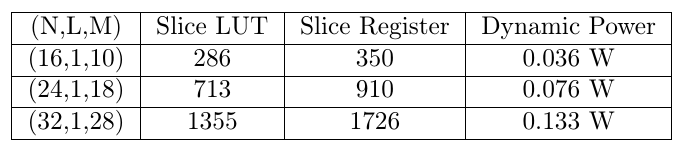
Fixed Point Reciprocal Computation IP achieves higher frequency but dynamic power is calculated at 200 MHz. This IP accepts unsigned numbers but it can be used for signed numbers easily by just placing two’s complement blocks before and after this block. This block has latency of (L+M) clock cycles which is lower than that of a complete divider.

Application

1. Matrix factorization.
2. Linear equation solving.
3. Machine learning algorithms.

0

0