Signal processing algorithms can have square root operations along other arithmetic operations. Computational complexity of square root operation is higher than other arithmetic operations. But square root operation is some times can not be avoided and thus must be modelled by HDL. This product is basically a Fixed Point Square Root IP which is capable of computing square root of any number of maximum width 64.
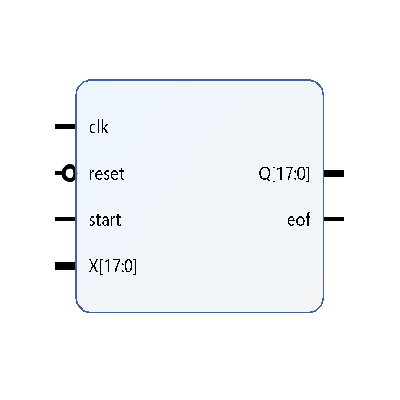
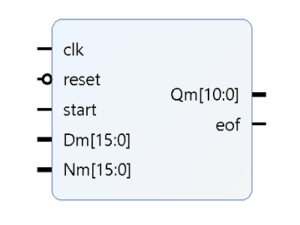
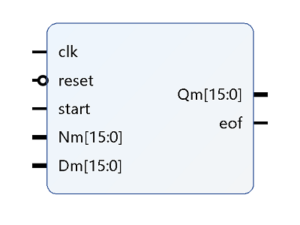
This block has two parameters N and M. N represents the data width of the input data and M represents the precision in the fixed point data format. For example, in a 16-bit architecture 10-bits are used to represent the fractional part. The architecture of this IP is based on the non-restoring radix-2 philosophy. Thus both N and M should be even and together (N+M) can be maximum of 64.
This block has three 1-bit signals, clock, reset, start. Start pulse is synched with the first input data. This IP has two outputs, Q and eof. The pulse eof indicates that square root block is giving output and this pulse is synched with first output. Basically, eof signal is delayed version of start pulse to track the result.
The IP is tested on Xilinx XC7A35T-1FTG256 Artix 7 FPGA which has 50 MHZ onboard clock oscillator. The inline logic analyzer (ILA) which inbuilt IP of Vivado is used to verify Fixed Point Square Root IP. Hardware resource of this block is shown below
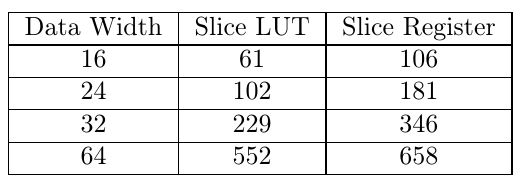
Frequency analysis of this block is also carried out. It achieves around 500 MHz when used alone. But we are not stressing on this result as in real this IP is not tested at this frequency. More reasonable result for this IP (N = 18, M=10) is that it consumes 0.104 W dynamic power when operated at 200 MHz. Latency of this block is (N+M)/2 -1 number of clock cycles.

Reviews
There are no reviews yet.