Verilog Code for Back Propagation to Solve Triangular Linear System

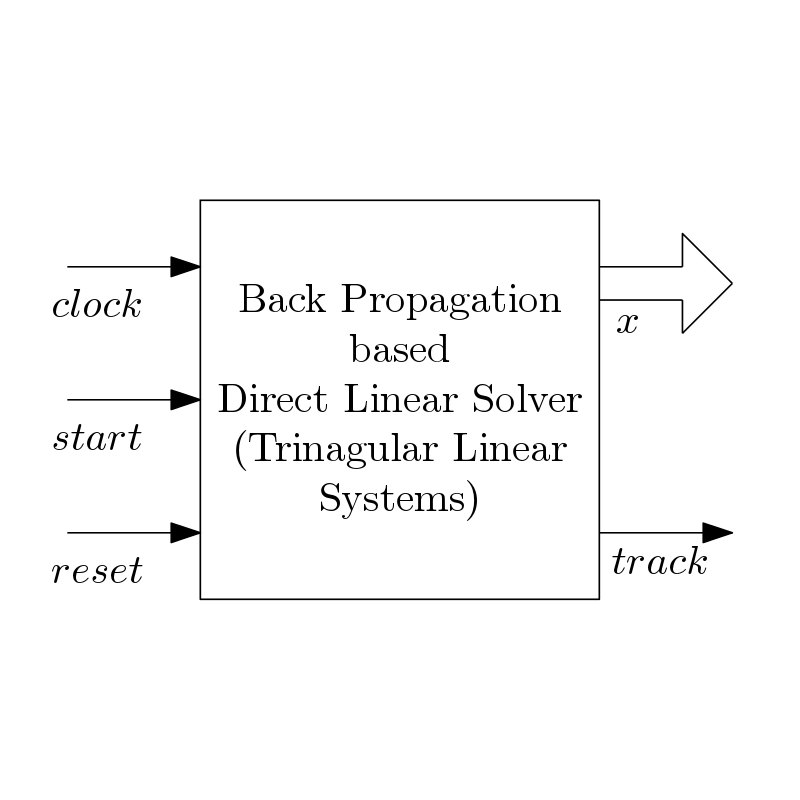
Back propagation or back substitution is one of the important techniques to solve linear system when the co-efficient matrix is triangular. Back propagation or forward propagation can be applied when the matrix is either upper triangular or lower triangular. These means, for triangular systems, regular linear system solution techniques are not required to apply.

Here, Verilog codes for three kinds of architectures are given which are

1. Back Propagation Architecture 1: This architecture is suitable when the matrix is upper triangular with non-zero diagonal elements. Basically, this kind of matrices are produced in case of QR decomposition. After QR, back propagation can be easily applied to solve the linear system.
2. Back Propagation Architecture 2: This architecture is suitable when the matrix is upper triangular with unity diagonal elements. Means all diagonal elements are equal to 1. Basically, this kind of matrices are produced in case of Gaussian Elimination (GE). After GE, back propagation can be easily applied to solve the linear system.
3. Back Propagation Architecture 3: This architecture is actually the modified version of back propagation architecture 2. This is a systolic version of back propagation architecture 2. Two submodules are designed here which simultaneously act on a bigger matrix.

All the architectures are Verified using Vivado simulator. These architectures use 18-bit data width with 10-bits of precision. Matlab code, sample memory files and Verilog codes are attached with the file. Simulation sample of all the architectures are also given in the zip file.

0

0