A linear system y=Ax can also be solved using a different matrix inversion bypass (MIB) technique. Here, inverse of a matrix is not calculated directly. Instead, inverse is calculated by block wise. This technique is based on Schur-Banasiewicz block wise matrix inversion algorithm [1].
In this work, a prototype of the linear solver using MIB technique is given. This architecture is easily scalable to any parameter. The co-efficient matrix size is 8*4, the size of measurement matrix is of 4*1, and thus the size if x is also 4*1. The measurement matrix is stored in a ROM.
The architecture uses maximum hardware sharing to have minimum resource consumption. Architecture uses 18-bit data width, and precision is of 10-bits. The simulation of this architecture is
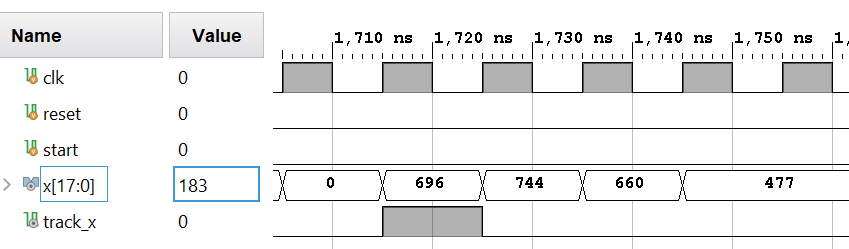
The track_x pulse is used to track the output estimation. The architecture is fully synchronous and designed with Verilog HDL with every block parameterized. The architecture is verified with VIVADO 2019 version and targeted to artix 7 fpga device.
[1]. G. Huang and L. Wang, “High-speed signal reconstruction with orthogonal matching pursuit via matrix inversion bypass,” in IEEE Workshop on Signal Processing Systems, Oct 2012, pp. 191–196.


Reviews
There are no reviews yet.